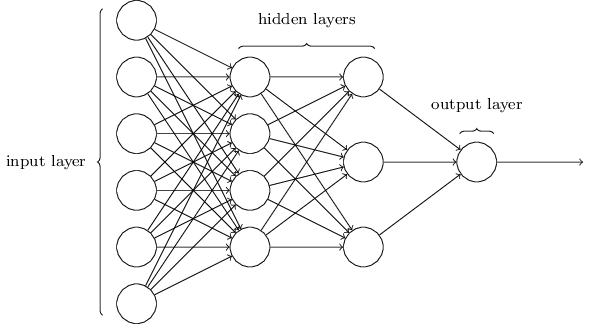
Neural Networks and Deep Learning 学习笔记二：

学习

Deep Learning重点自然在于学习，通过让神经网络学习，来达到我们想要的功能。

学习算法听起来很棒。 我们如何为神经网络设计这样的算法？

假设我们有一个感知器网络，我们想用来学习来使感知机网络可以解决一些问题。 例如，网络的输入可能是来自数字扫描的手写图像的原始像素数据。 我们希望感知机网络学习权重和偏差，以便网络的输出正确地对数字进行分类。

假设我们在网络中的一些权重（或偏差）中做了一个小的改变。 我们想要的是这个小的权重变化只会导致网络输出的相对较小的变化。 我们稍后会看到，这个属性将使学习成为可能。 理论上，这就是我们想要的（当然这个网络太简单了，无法做手写识别！）：

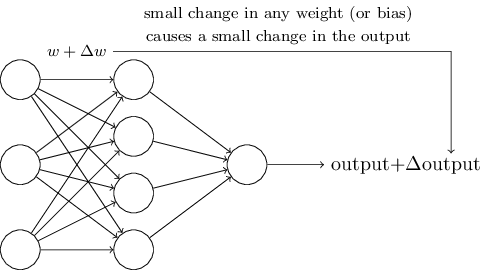
如果权重（或偏差）的微小变化只会导致输出的微小变化，那么我们可以使用这个前提来修改权重和偏差，以使我们的网络可以达到我们要想到功能。 例如，假设网络错误地将图像“9”分类为“8”。 我们可以在权重和偏差上做一个小的改变，这样网络可以更接近地将图像分类为“9”。 改变权重和偏差，以产生更好的输出， 这就是网络在学习。

事实上，网络中任何单个感知器的权重或偏差的小小变化有时可能导致该感知器的输出完全翻转，例如从0到1。然后，这种翻转可能导致网络其余部分会以一些非常复杂的方式完全改变，这样得到我们想要的输出会非常的困难。

Sigmoid neurons

我们可以通过引入Sigmoid neurons来解决这个问题。Sigmoid neurons与感知器类似，但是其权量和偏差的微小变化只会导致其输出的微小变化。 这就是Sigmoid neurons能够学习的关键所在。

像感知器一样，Sigmoid neurons有输入，x1，x2，… 不仅仅是0或1，这些输入可以在0和1之间取任何值，例如，0.638 …

和感知器一样，Sigmoid neurons对于每个输入有权重w1，w2，… 和偏差b，输出不是0或1，而是$\sigma(w·x + b)$，其中$σ$称为Sigmoid函数：

\begin{eqnarray} \sigma(z) \equiv \frac{1}{1+e^{-z}}. \tag{1}\end{eqnarray}

更明确地说，输入x1，x2，…，权重w1，w2，…和偏差b的Sigmoid neurons的输出是：

\begin{eqnarray} \frac{1}{1+\exp(-\sum_j w_j x_j-b)}. \tag{2}\end{eqnarray}

看起来Sigmoid neurons和感知机有很大区别，实际上它们是非常相似的。首先，我们先看Sigmoid函数$\sigma()$的图像:

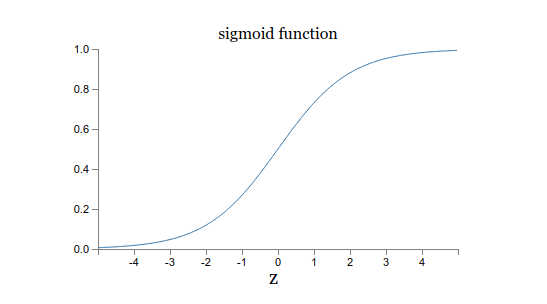
假设$z≡w⋅x+b$是一个非常大的正数，那么$e^-z\approx{0}$ 并且$σ(z)≈1$。换句话说，当$z=w⋅x+b$非常大并且为正数，sigmoid neurons的输出结果接近于1, 就像感知器一样。 假设$z=w⋅x+b$是非常大的负数，则有$e^{-z}\rightarrow\infty$, 并且$σ(z)≈0$。即当$z=w⋅x+b$非常大并且为负数，就像感知器一样，sigmoid neurons的输出结果接近于0。因此只有当$w⋅x+b$具有适度的大小时，才有与感知器模型有很大的偏差。

这种形状可以认为是阶梯函数的平滑版本：

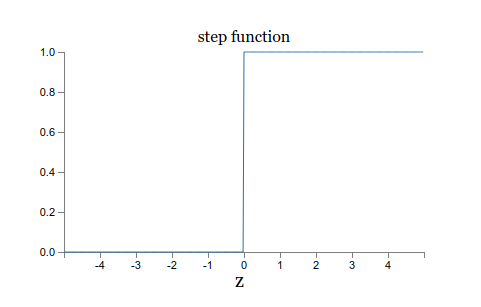
如果$σ$是一个阶梯函数，那么Sigmoid neurons将成为感知器，因为输出为1或0，取决于$w·x + b$是正还是负。

但是实际上，当w⋅x+ b = 0时，感知器输出0，而step函数输出1。所以严格来说，它们还是有一点区别的

---

Sigmoid neurons 可以像感知机一样，根据 w (weight权重) 和 b (bias偏差)来引起输出的微小变化，这样Sigmoid neurons才能够完成学习，如下所示：

\begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b \tag{3}\end{eqnarray}

Sigmoid neurons的输出$\sigma(w·x + b)$可能会是0.731，0.293等等，我们可以通过判断输出是否大于某个特定的值，例如0.5，将输出分为1或者0，完成分类。

\begin{eqnarray} \mbox{output} = \left\{ \begin{array}{ll} 0 & \mbox{if } \sigma(w \cdot x+b)\leq 0.5 \\ 1 & \mbox{if } \sigma(w \cdot x+b) > 0.5 \end{array} \right. \tag{4}\end{eqnarray}

之后，会有如何根据输出的结果与预期的结果，用一些算法，例如后向传播算法，来调整$w$ (weight)和$b$ (bias)，让我们的网络可以完成我们想要的功能。

神经网络的结构