Neural Networks and Deep Learning 学习笔记三:
目录
开始
识别诸如此类的手写数字问题,由两个子问题构成,一则是分离这些数字,将它们分为如下的单独的数字,再对每一个数字进行识别

二就是识别单独数字了,比如从第一个数字开始,对我们人类来说很容易就能看出来这是5。
对于神经网络来说,我们关注第二个问题,识别(或者说归类)单独的数字。
网络
在这里,我们使用如下的一个三层神经网络来进行手写体识别
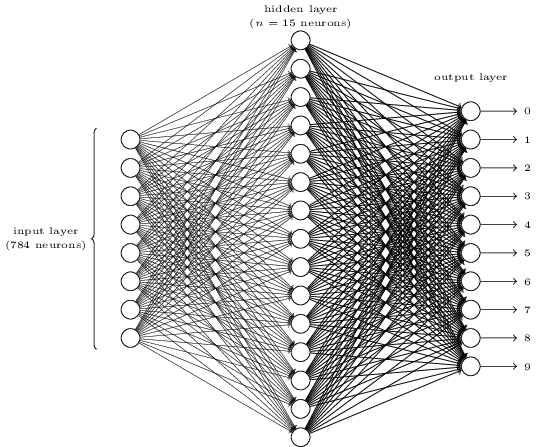
网络的输入是已编码的像素值。由于神经网络的训练数据由扫描手写数字图像(28×28)组成,因此输入层包含784 = 28×28个神经元。同时,输入像素为灰度值,值为0.0时,表示白色,值为1.0时,表示黑色,在这中间的值自然表示逐渐变暗的灰色。
网络的第二层是隐藏层。我们用n表示这个隐藏层中的神经元数,将用n来验证不同的值对神经网络的影响。 所示的示例示出了仅包含n = 15个神经元的隐藏层。
网络的输出层包含10个神经元。使用one-hot编码。
如果第一个神经元触发,即输出≈1,那么这将表明网络认为数字是0。如果第二个神经元被触发,那么这将表明网络认为数字是1,以此类推。更准确地说,我们将输出神经元从0到9编号,并计算出哪个神经元具有最高的触发值。
在这里输出之所以不用4个神经元以二进制的方式来表示输出,而用10个, 最终的理由是经验性的:我们可以尝试两种网络设计,事实证明,对于这个特定的问题,具有10输出神经元的网络学习比具有4个输出神经元的网络更好地识别数字。
首先考虑使用10个输出神经元的情况。
让我们集中精力在第一个输出神经元,这个是试图决定数字是否为0的神经元。而输出的结果是通过隐藏层神经元来实现的。隐藏层中的第一个神经元会检测是否存在如下图像:

它可以通过对与上图有重叠部分的输入像素进行重量加权,并且只对其他输入进行轻量加权来做到这一点。 以类似的方式,隐藏层中的第二,第三和第四个神经元检测是否存在以下图像:

您可能已经猜到,这四个图像一起构成了我们在前面显示的数字中看到的0的图像:

所以如果所有这四个隐藏的神经元都在触发,那么我们可以得出结论,数字是一个0。至少在这种情况下,我们得出结论,输入是0。
假设神经网络是以这种方式的话,我们可以给出一个合理的解释,为什么最好从网络中输出10个输出,而不是4。
假设我们使用4个输出神经元,则第一个输出神经元将尝试确定该位的最高有效位,例如:4, 最高有效位为0(0100)。而且没有简单的方法可以将最高有效位与上面所示的简单形状联系起来。
也许有一个很不错的学习算法会找到一些权重的赋值,让我们只使用4个输出神经元来完成识别。
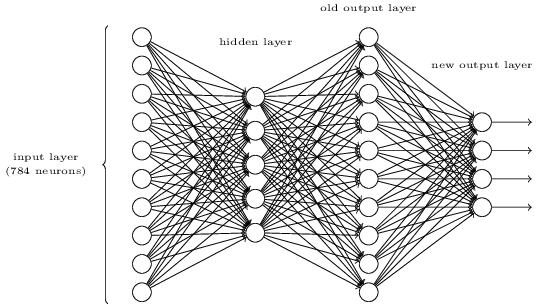
当然,也存在通过向上述三层网络添加额外层,来确定数字的按位表示的方法。 额外的层将上一层的输出转换为二进制表示。
用梯度下降( gradient descent)的方法来学习(learn)
现在需要的事找到是学习的数据集,即所谓的训练数据集。 使用MNIST数据集,其中包含数以万计的手写数字扫描图像及其正确的分类。 当然,当测试我们的网络时,我们会要求它识别不在训练集中的图像。
MNIST数据分为两部分。 第一部分包含60,000张图像作为训练数据。这些图像是灰度图像,大小为28×28像素。 MNIST数据集的第二部分是要用作测试数据的10,000张图像,同样也是28乘28灰度图像。 使用测试数据来评估我们的神经网络学到如何识别数字。