Python代码：GitHub

简介

复杂网络

在网络理论的研究中，复杂网络是由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构。用数学的语言来说，就是一个有着足够复杂的拓扑结构特征的图。复杂网络具有简单网络，如规则网络、随机图等结构所不具备的特性，而这些特性往往出现在真实世界的网络结构中。

在自然界和人类社会中，复杂网络无处不在，如自然界中的生态网络、新陈代谢网络、蛋白质网络等；人类社会中的社交网络、交通网络、电子邮件网络、科学家合作网、电子电路网络等，这些复杂系统都可以用复杂网络的相关特性进行描述和分析，网络中的结点表示系统个体，边表示个体之间的关系。如今，复杂网络的研究是现今科学研究中的一个热点，它已渗透到各个领域，并成为这些领域的重要研究方向。

社区发现

随着复杂网络理论的发展，继1998年Watts和Strogtz提出了WS小世界模型(Small-world network)，1999年Barabasi和Albert提出无标度网络模型(Scale-free network)之后，人们发现复杂网络具有一定的社区结构。相同类型节点之间连接较多，构成一个一个的小社区，不同类型节点之间连接较少，但成为沟通不同社区的重要通道，这种连接的不均匀性表明，网络内部存在一定的自然分化。

对于社区（community），目前没有明确的定义，常见的是Newman和Gievan提出的：社区是图的一个子图，相比于图的其他部分，其中包含着密集的节点，或者等价地说，如果图一个子图内部的链接数量高于这些子图之间的链接数，我们就可以说这个图含有社区。如下图所示，图中网络包含三个社区结构，分别对应图中的三个虚线圈内的节点，同一社区内的节点和节点之间连接很紧密，而社区与社区之间的连接比较稀疏。换而言之，复杂网络的社区结构是复杂网络中社区之间的连接相对稀疏，而社区内部的连接相对稠密的特性。

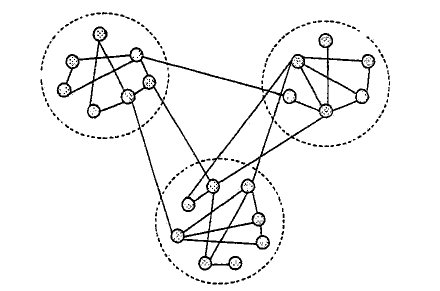
介数和边介数

一种复杂网络中社区发现的方法是寻找位于社区之间的边，如果能找到并移除这些边，最终将只剩下孤立的社区。

谈及一条位于社区之间的边，由于与多方法可以对其量化，并基于此实现社区发现算法。2004年，Newman和Girvan的论文中提出了利用介数中心性（betweenness centrality）的方法，称之为Girvan-Newman算法，这篇论文也是开创了社区发现这一领域的文章。本文主要针对无权和有权网络，对此类算法进行一定的研究分析。

在图论中，介数中心性（betweenness centrality）是基于最短路径的图的中心的度量方法。对于连通图中的每对顶点，在顶点之间至少存在一条最短路径，而一个节点的介数一般是指通过该节点的最短路径数。

介数中心性的定义为：

$C_B(v)= \sum_{s\ne v\ne t \in V}{\frac{\sigma_{st(v)}}{\sigma_{st}}}$

​
　　其中 $σ_st(v)$ 表示经过节点v的s→t的最短路径数，$ σ_st $ 表示s→t的最短路径数。直观上来说，介数中心性反映了节点v作为“桥梁”的重要程度。因此，我们可以定义边介数（edge betweenness）为经过该边的最短路径数，如图1所示，位于社区之间的边的边介数将会很大。同时，可以进一步得到边介数中心性（edge betweenness centrality）。

社区发现的衡量标准——模块度函数Q

Newman和Girvan针对社区发现问题的同时，提出了模块度函数 $Q$ 来定量的衡量社区划分的结果。该度量标准自提出以来，逐渐被大多数研究者们接受，并发展了很多以模块度为目标函数的新算法。

模块度，是指复杂网络中连接社区内部节点的边所占的比例，与另一个随机网络中连接社区内部节点的边所占的比例的期望值的差值。其中，这个随机网络的构造方法为：保持每个节点的社区属性不变，根据节点度对节点间的边进行随机连接。如果社区结构比较明显，则社区内部连接的边的比例应改高于随机网络的期望值。

因此，可以用模块度函数 $Q$ 定量描述社区划分的模块化水平。假设已经发现复杂网络的社区结构，$M$ 为已发现的社区个数，$L$ 为网络中的边数，$l_s$ 是社区 $s$ 中节点相互连接的数目，$d_s$ 是社区 $s$ 中所有节点相互连接数目的和。则 $Q$ 的函数表达式如下所示：

$Q = \sum_{s}^{M}{\left[\frac{l_s}{L}-(\frac{d_s}{2L})^2 \right]}$

上式的物理意义是：网络中连接两个同种类型的节点的边（即社区内部边）比例，减去在同样的社区结构下任意连接这两个节点的边的比例的期望值。如果社区内部边的比例不大于任意连接时的期望值，则有 $Q=0$ ， $Q$ 的上限为1，而 $Q$ 越接近这个值，就说明社区结构越明显，在实际网络中， $Q$ 值常位于0.3和0.7之间。

基于介数的社区发现的经典算法——Girvan-Newman算法

基于边介数的社区发现算法

这样的社区发现算法的主要思路为：计算网络中所有边的边介数，然后寻找边介数值最大的边并移除。在移除时，会改变一些边的边介数。以前经过被移除边的最短路径，现在改为经由其他边，因此必须重新计算边介数，然后再次搜索值最大的边并移除，依此类推。当一条接一条边被移除时，最初连通的网络最终会被分成两部分、三部分等等，直至网络的每一个成为一个社区，是一种分裂算法。

算法的执行过程可用树状图表示，如下图所示。算法从顶部开始生成树状图，首先是单个连通网络，然后将其不断划分，直至每个分支只有单个结点为止。在算法运行期间，每个独立的网络结构状态对应于树状图的水平切分，在图2中用红线表示。与红线相交的每个分支代表一组节点，即一个社区，沿分支向下到底部的全部节点都为其成员。因此对于一个连通网络，树状图能够得到算法执行全过程中每个阶段里网络划分的社区结构。

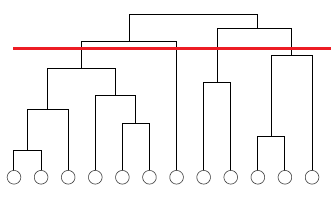
这样我们可以发现，这种算法并不是给出将网络划分成社区的唯一划分，而是给出多种不同程度的划分。范围比较粗的划分，将网络划分为几个大的社区，范围比较细的划分，将网络划分为许多比较小的社区。这种不同程度的划分，可以揭示关于层次网络结构的信息。同时，用户可根据目标社区数来决定进行哪些划分，或者利用模块度函数 $Q$ 给出该算法的最优划分。

Girvan-Newman算法

如前所述，直观来看，在社区内部节点之间相互连接的边密度较大，因此，通过边介数（连接社区的边的边介数大）来识别社区是一种较为直观的社区发现算法。Girvan-Newman算法即是一种基于介数的社区发现算法，其基本思想是根据边介数中心性（edge betweenness）从大到小的顺序不断的将边从网络中移除直到整个网络分解为各个社区。因此，Girvan-Newman算法实际上是一种分裂方法。

Girvan-Newman算法的基本流程如下：
（1）计算网络中所有边的边介数；
（2）找到边介数最高的边并将它从网络中移除；
（3）重复步骤2，直到每个节点成为一个独立的社区为止，即网络中没有边存在。

Girvan-Newman算法给出了如何除去边得到社区结构。但在得到最终的社区数之前，还有一个问题没有得到解决，即如何确定合适的社区数，使社区划分结果最优。这时需要用到之前提到的衡量标准——模块度函数 $Q$ 。

这样可以利用 $Q$ 值寻找合适的社区数，Girvan-Newman算法中每去除一次边，则计算一下所得社区结构的 $Q$ 值，寻找到 $Q$ 值最大时的社区数量。如下图所示，当边去除后，社区数量为4时，所得 $Q$ 值最大，因此该网络划分为4个社区最优。

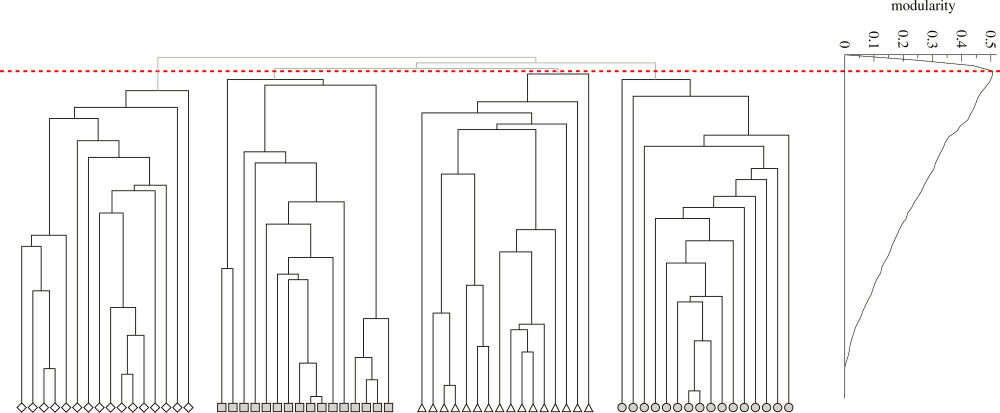
Python实现

Python代码：GitHub

Zachary’s karate club网络

Zachary网络是一个检验不同社区发现算法的经典真实的无权网络，一共有34个节点，78条边。该网络是Zachary在上世纪70年代，用了两年时间观察研究空手道俱乐部34个成员之间的个关系而得到的，如下图所示。在调查过程中，俱乐部的主管和校长产生争执，分裂成了两个团体，真实的社区如下所示：

[[1, 2, 3, 4, 5, 6, 7, 8, 11, 12, 13, 14, 17, 18, 20, 22], 
[32, 33, 34, 9, 10, 15, 16, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31]]

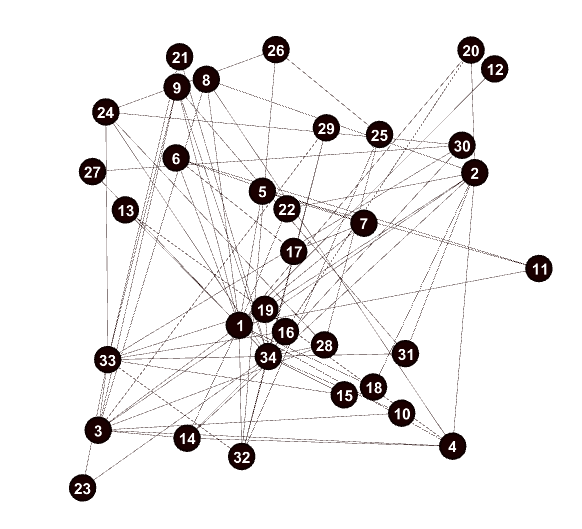
这里使用 Python 的 NetworkX 包以及 Matplotlib 包来完成对于 Girvan-Newman 算法的演示，以及Gephi，一个基于JVM的可视化平台。

NetworkX是一个用于创建，操作和研究复杂网络的结构、动态和功能的Python包。Matplotlib是一个Python 2D绘图库，利用它完成模块化函数Q与划分社区数目的关系曲线，之后使用Gephi作为网络的可视化工具，将GML文件中的图中划分的社区表示出来。

Python环境需求：
1. Python-3.6.3
2. NetworkX-2.0
3. Matplotlib-2.1.0

安装好Python环境需求后，可直接运行Girvan-Newman.py，输出格式为GML的文件，以及其他信息。获得基于Girvan-Newman算法的社区发现的一些特性。Zachary’s karate club网络Girvan-Newman算法划分社区数与Q值的关系（如下图所示）。

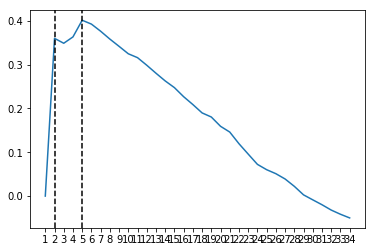
我们可以看到，当我们已知应该划分社区的个数，即2个社区时，Girvan-Newman算法的模块度函数Q值到达极大值，为0.35996055226824464，将输出的GML文件用Gephi打开。这时的社区划分结果如下所示，除了节点3以外,其它节点都被正确归类，如下图所示。

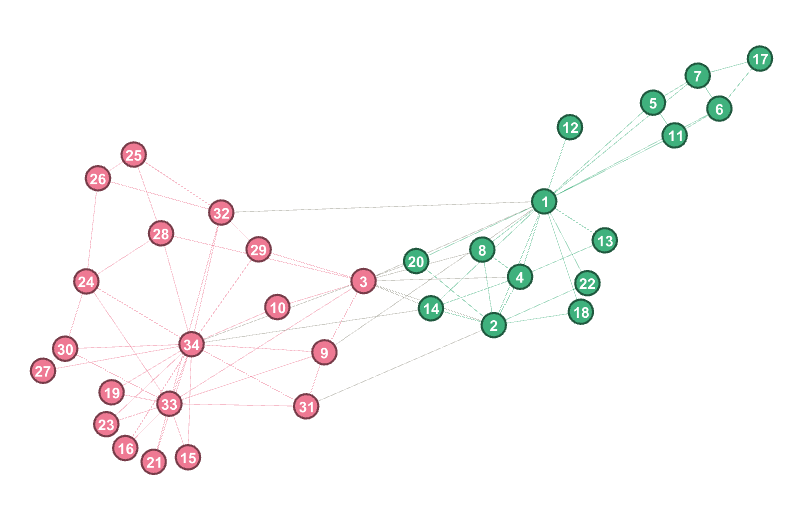
-----------Using number to divide communities and the Q-----------
The number of Communites: 2
Communites: [[1, 2, 4, 5, 6, 7, 8, 11, 12, 13, 14, 17, 18, 20, 22], [32, 33, 34, 3, 9, 10, 15, 16, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31]]
Max_Q: 0.35996055226824464
-------------------------------------------------------------------

但是对于不知道应该划分社区个数时，依赖模块度函数Q的最大值划分社区，从图3中可知，当划分成5个社区时，模块度函数Q达到最大值，为0.40129848783694944，这时的社区划分结果较实际网络相差略大。

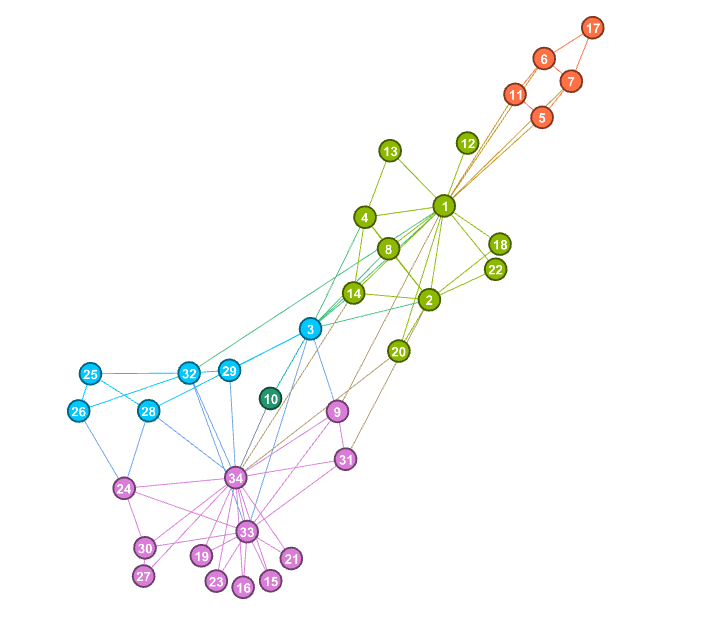
-----------the Max Q and divided communities-----------------------
The number of Communites 5
Communites: [[1, 2, 4, 8, 12, 13, 14, 18, 20, 22], [32, 3, 25, 26, 28, 29], [5, 6, 7, 11, 17], [33, 34, 9, 15, 16, 19, 21, 23, 24, 27, 30, 31], [10]]
Max_Q: 0.40129848783694944
-------------------------------------------------------------------

下图为 Newman和 Girvan 在论文 Finding and evaluating community structure in networks 中给出计算结果，和之前给出的图以及计算出的划分社区的每一个步骤对比发现，我们实现的Girvan-Newman算法与论文中给出的结果相一致。

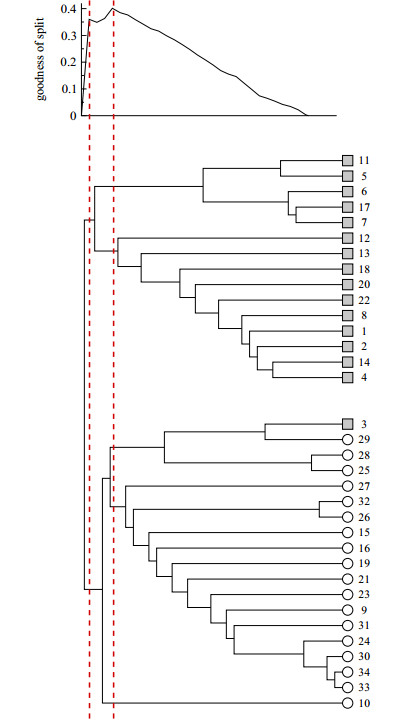
Girvan-Newman算法分析

对于$m$条边和$n$个节点的网络，Girvan-Newman算法计算边介数的时间复杂度为$O(n(m+n))$，且在移除$m$条边的每条边前都需要执行该计算，所以整个算法的时间复杂度为$O(mn(m+n))$。

若在$m∝n$稀疏网络中的时间复杂度为$O(n^3 )$。

这里总结下Girvan-Newman算法的优缺点。

Girvan-Newman算法的优点：

1. 在知道划分社团数量时，可以较为精确的给出社团的划分结果；
2. 可以给出不同程度的社团划分结果，可以揭示关于网络层次结构的信息；

Girvan-Newman算法的缺点：

1. 在计算边介数的时候可能会有很多重复计算最短路径的情况，时间复杂度太高；
2. 若无法知道应该划分社团的数量，算法效果会相对较差；

总而言之，Girvan-Newman算法不必依赖多余的信息来判断得到的社团结构是否具有实际意义,而是可以直接从网络的拓扑结构来进行分析。

但是该算法的耗时比较大，时间复杂度为$O(mn(m+n))$，因此它仅仅适用于中等规模的复杂网络$(n≤10000)$。

参考文献

1、Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical review E, 2004, 69(2): 026113.
2、杨晓光. 基于复杂网络的社区发现算法研究与实现[D].南京理工大学,2017.
3、汪洋. 复杂网络的社团发现算法研究[D].安徽大学,2014.
4、莫春玲. 复杂网络中聚类方法及社团结构的研究[D].武汉理工大学,2007.