Introduction 介绍

当图像要用于分析图像中的不同区域（如目标识别）时，减少图像中的数据量，同时保留重要的特征结构信息是非常重要的。

边缘检测（Edge Detection）可以显着减少图像中的数据量。然而，边缘检测器的输出仍然是由像素描述的图像。 如果线条，椭圆等可以通过它们的特征方程来定义，那么数据量将会减少得更多。

Hough变换最初是为了识别直线（Line）而开发的，并且后来被广义化为涵盖任意形状。

Hough space and Hough Transform 霍夫空间与霍夫变换

直线在 Hough space 中的表示

直线可以唯一地由两个参数来表示，经过点 (x,y)(x, y) 的直线可表示为：

\begin{equation} y=a·x+b \tag{1} \end{equation}

其中参数 aa 为斜率, bb 为截距，通过点 (x,y)(x,y) 的直线有无数条，且对应于不同的 aa 和 bb 值, 如果将 xx 和 yy 视为常数，而将原本的参数 aa 和 bb 看作变量，则 (1) 可以表示为：

b=−x⋅a+yb=-x·a+y

这样直线 y=a⋅x+by=a·x+b 就变换到了参数为 (a,b)(a,b) 的 Hough 空间，这就是直角坐标系中对于 (x,y)(x,y) 点的 Hough Transform 霍夫变换。

我们可以发现在直角坐标系(即欧式空间)中的一条直线，对应于 Hough 空间中的一个点，如下图所示

1

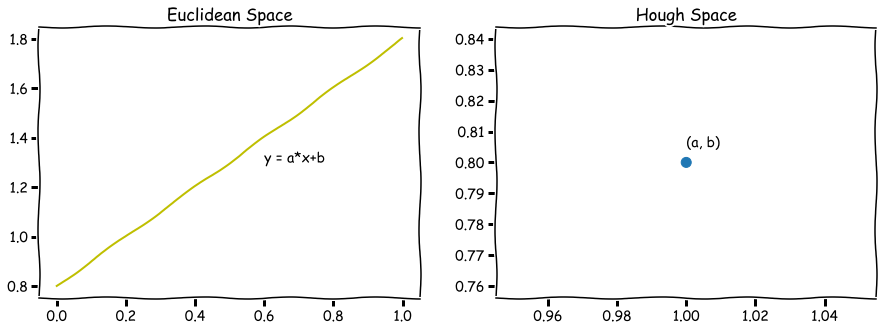
欧式空间中的一条直线对应于Hough空间中的一个点，反过来Hough空间中的一条线自然对应于欧式空间的一个点，如下图所示

2

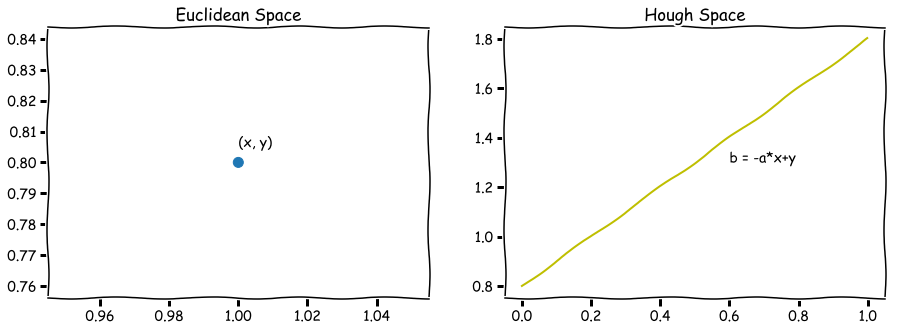
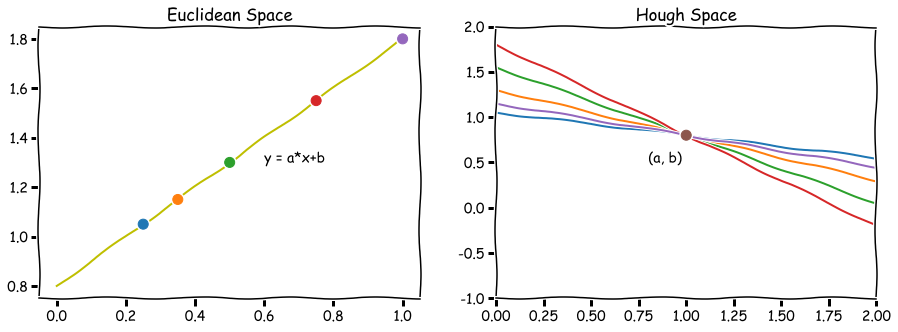
这时我们就可以想到，对于欧式空间的多个点，映射到Hough空间，即为多条直线。

如果我们可以找到一条穿过这些点的直线，每个点映射到Hough空间的线必然相交于一个点，而这个点就是我们需要的直线参数，即完成了对于直线的检测。

3

极坐标系下

上面的内容已经将Hough变换检测直线的原理呈现出来了，但是在直角坐标系下的表示形式，存在无法表示垂直于x轴的直线的问题，此时a=∞a=\infty

所以我们将(1)改写为极坐标表示：

\begin{equation} r=x·cos\theta + y·sin\theta \tag{2} \end{equation}

并保持与 (1) 的形式一致:

\begin{equation} y=-\frac{cos\theta}{sin\theta}·x+\frac{r}{sin\theta} \tag{3} \end{equation}

当θ∈[0,180]\theta \in [0, 180] 和r∈Rr \in \mathbf{R}（或者θ∈[0,360]\theta \in [0, 360]且 r⩾0r\geqslant 0）时，极坐标系中所有的直线都可以用这种形式表示。

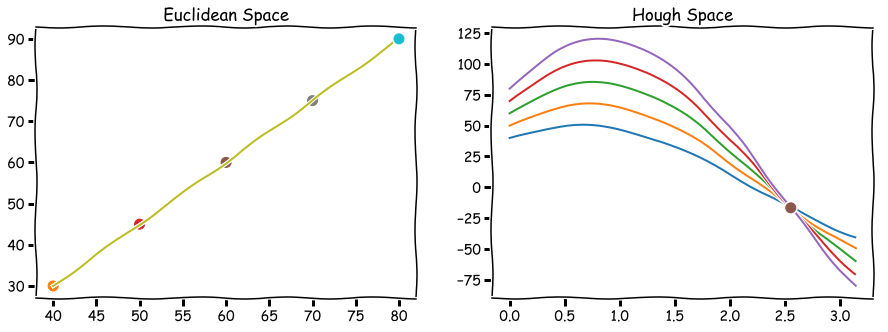
Hough空间因此具有这两个维度: θ\theta和 rr，并且极坐标系下直线由Hough空间的单个点表示，对应于唯一的一组参数（θ0\theta_0，r0r_0）

与直角坐标系相同，极坐标系下的多点，对应于Hough空间中的多个曲线，若存在过这些点的一条直线，则Hough空间中的曲线必然相交于一点。

4

Algorithm 算法

Transformation to Hough Space

如之前所述，每个edge point被转换成Hough空间中的一条线，并且大多数Hough空间线，相交的区域在Edge Image中对应于一条直线。

即欧式空间中可能被拟合为一条直线的多点，对应于与Hough空间中的多条线，并且这些线可以相交于一点，该点参数即为欧式空间中直线的参数；

同理，如果可以拟合成多条直线，则Hough空间中必定存在多个曲线相交的点。

The Hough Space Accumulator

为了确定霍夫空间中大多数线相交的区域（点），使用一个覆盖Hough空间的累加器（Accumulator）

当一个Edge point被转换到Hough空间时，对于Hough空间位置的累加器的值增加,同时也很好理解，累加器的分辨率决定了检测直线的精度。

这样我们也可以看到，累加器的维数对应于Hough变换问题中未知参数的个数。

对于椭圆而言，需要5个参数（其中心的坐标，其主轴和副轴的长度以及角度）,对于直线，只需两个维度（rr 和 θ\theta）就足够了

Detection of Infinite Lines

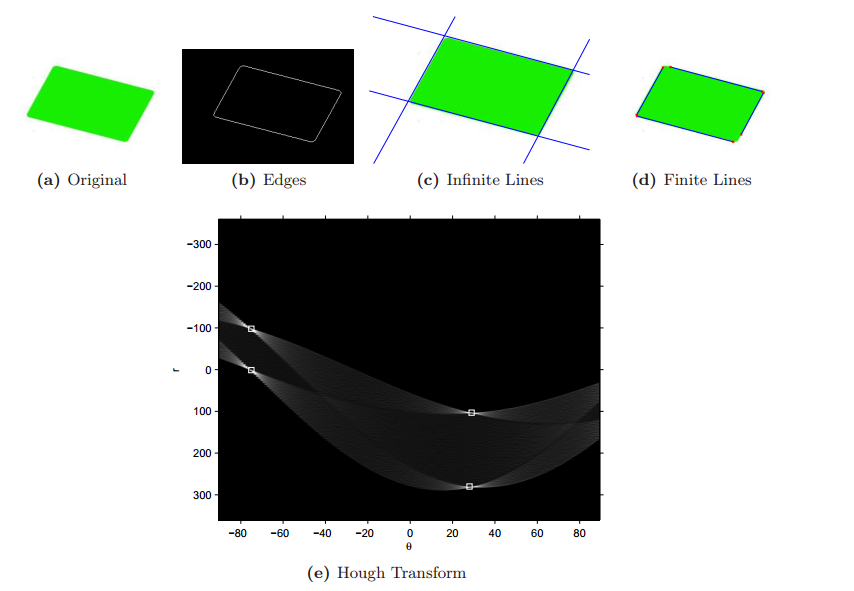
当所有Edeg points 已经被转换到Hough空间时，通过检测累加器的值来检测直线。

检测直线最基本的方法是为累加器设置一些阈值，然后保留高于阈值的值。阈值可以是累加器中最大值的50％，这种方法偶尔可以满足要求，但在许多情况下，必须采用其他的约束条件。

从下图中可以看出，Hough Transform累加器最大值周围的点，也具有较大的值。因此，仅设置一个简单的阈值，将会检测到与真实直线相近的多个直线。

为了避免这种情况，可以定义一个抑制邻域的方法，这样在检测到两条线之前，必须有两条线显著的不同。

5

Finite line

经典的Hough transform检测仅由参数 rr 和 θ\theta给出直线，并且没有关于长度的信息。 因此，所有检测到的线的长度都是无限的。

如果需要有限长的直线，则必须执行一些附加分析以确定图像的哪些区域存在直线。

有以下几种算法：

  • 一种方法是存储累加器中所有点的坐标信息，并使用这些信息来限制线条。 但是，这会导致累加器使用更多的内存。
  • 另一种方法是沿Edge图像中无限长的直线搜索以找到有限长度的直线。 这种方法的一种变体称为 Progressive Probabilistic Hough Transform（渐进概率霍夫变换）

Progressive Probabilistic Hough Transform 渐进概率霍夫变换

霍夫变换不是一个查找图像中长度无限的线快速算法，由于需要附加的分析以检测长度有限的线，则会更慢。加快Hough变换算法速度，并同时寻找长度有限的直线的方法是 Progressive Probabilistic Hough Transform渐进概率霍夫变换（PPHT）

这种方法的想法是将Edge图像中随机选择的像素，转换到累加器。 当在累加器可确认一个特定的无限长度的直线时，沿该条直线搜索Edge图像，以查看是否存在一个或多个有限长度的线。

然后在该直线的所有像素被从Edge图像中除去。通过这种方式，算法返回有限长度的直线。 如果搜索阈值较高，则在累加器中评估的像素数量会变小。

该算法可以概括如下：

  1. 创建输入边 Edge 图像（IMG1）的副本（IMG2）。
  2. 用从 IMG2 随机选择的像素更新累加器。
  3. 从 IMG2 中删除像素。
  4. 如果修改的累加器（BINX）中具有最大值的较低阈值，转到第1点。
  5. 沿着由BINX指定的线在 IMG1 中搜索，找到连续或间隙不超过给定阈值的间隔的最长像素段。
  6. 从 IMG2 中删除段中的像素。
  7. 清除BINX。
  8. 如果检测到的线段比给定的最小长度长，请将其添加到输出列表中。
  9. 转到第2点

问题

该算法的一个问题是，多次运行可能会产生不同的结果。 如果许多直线共享像素，则会出现这种情况。

如果两条线交叉，要检测的第一条线将去除公共像素（以及其周围的部分），从而导致另一条线上出现凹陷。 如果多条线交叉，则许多像素可能会错过最后一行，并且累加器中的投票可能无法达到阈值。

步骤与应用

直线检测算法可以分为以下几个步骤：

  1. 边缘检测（edge detection），例如：Canny edge detection
  2. 将edge point映射到霍夫空间并存储在累加器中。
  3. 通过阈值和可能的其他限制，寻找累加器中最合理的点（例如，寻找累加器中值最大的一点 或者 大于阈值的点），产生无限长度的直线。
  4. 将无限长度的直线转换为有限长度，并重叠在原始图像上。

Hough Transform 霍夫变换本身应用在第2点

opencv 以及 skimage 库都实现了 Hough transform 以及 ** Progressive Probabilistic Hough Transform** ，以直接调用其提供的算法接口。

1
2
3
4
5
6
7
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('building.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
plt.imshow(gray, cmap='gray')
plt.show()

6

1
2
3
4
5
6
# Using canny edge detection
low_threshold = 50  # Canny edge detection low threshold
high_threshold = 200  # Canny edge detection high threshold
edges = cv2.Canny(gray, low_threshold, high_threshold)
plt.imshow(edges, cmap='gray')
plt.show()

7

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
rho = 1
theta = np.pi / 180
threshold = 100
min_line_length = 30
max_line_gap = 10

def draw_lines(img, lines, color=[255, 0, 0], thickness=2):
  for line in lines:
    for x1, y1, x2, y2 in line:
      cv2.line(img, (x1, y1), (x2, y2), color, thickness)

def hough_lines(img, rho, theta, threshold, 
                min_line_len, max_line_gap):
  lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]),
                          minLineLength=min_line_len, 
                          maxLineGap=max_line_gap)
  line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)
  draw_lines(line_img, lines)
  return line_img


line_img = hough_lines(edges, rho, theta, threshold, min_line_length, max_line_gap)
plt.imshow(line_img, cmap='gray')
plt.show()

8

1
2
3
4
threshold = 10 # 修改门限值
line_img = hough_lines(edges, rho, theta, threshold, min_line_length, max_line_gap)
plt.imshow(line_img, cmap='gray')
plt.show()

9