增强RANSAC, Adaptive Parameter Calculation
目录
因为RANSAC不考虑所有可能的样本子集,RANSAC比确定算法运行速度更快,但是它的性能仍然可以通过一些启发式改进。这里我们采用Adaptive Parameter Calculation(自适应参数计算)来增强RANSAC算法。
关于RANSAC可以参考我的这篇文章。
Adaptive Parameter Calculation
Adaptive Parameter Calculation(自适应参数计算)
自适应参数计算的主要思想是在运行时,计算内群(inliers) 的比例,然后根据新的 的值修改其他参数。
它不仅可以用于降低计算的复杂性,而且可以用于当数据集没有关于 的信息时。
自适应参数计算从最坏的情况开始计算 ,当找到一致集(consensus set)的数据样本在整个数据集中的比例高于当前 时,重新分配更好的值给 。之后用新的 来更新迭代次数 和最小一致阈值 。
例如,我们可以选择 ,这样迭代次数 为 ,最小一致阈值自然为 。
让我们考虑一个问题,当找到一个一致集具有一半的数据集样本时,这样此时的 比开始对 的估计要好,所以将 更新为0.5,并重新计算 和 的值。同时由于 的值较高, 肯定会减少,所以改进后的RANSAC算法会在不失去其原有可靠性的前提下,提前结束。
此外, 被更新,并且会变为一个更大的值,这将会使用更少的一致集来拟合我们的模型。 因此,它隐含地降低了复杂性。
Basic Flow
以下是RANSAC的自适应参数计算的基本流程:
1 | k = infinity , i = 0 |
Python 实现
这里实现的时候要略微修改下原有的RANSAC代码
1 | # -*- coding: utf-8 -*- |
测试一下,我们实现的自适应参数的RANSAC效果:
1 | # -*- coding: utf-8 -*- |
1 | ============== Paramters =============== |
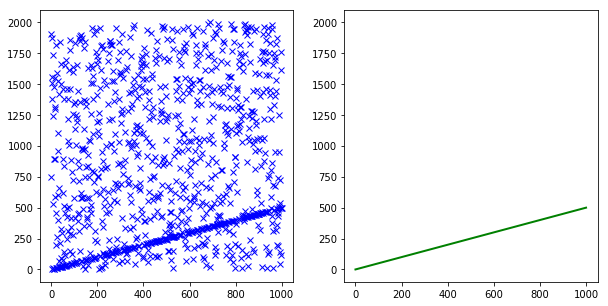
从迭代次数中,可以看出RANSAC的运行速度有了明显的提升
Reference
Wang, H., and D. Suter. “Robust Adaptive-Scale Parametric Model Estimation for Computer Vision.” IEEE Transactions on Pattern Analysis and Machine Intelligence 26, no. 11 (November 2004): 1459–74. https://doi.org/10.1109/TPAMI.2004.109.