Non-Maximum Suppression(NMS)非最大抑制
Intrduction
NMS(Non-Maximum Suppression),非最大(极大)抑制。
顾名思义,抑制不是最大值的元素,即抑制最大值以外的值,我们也可以理解为局部最大搜索。这里的局部可以代表一个有两个参数的邻域,一个参数为邻域的维度,另一个为邻域的大小。
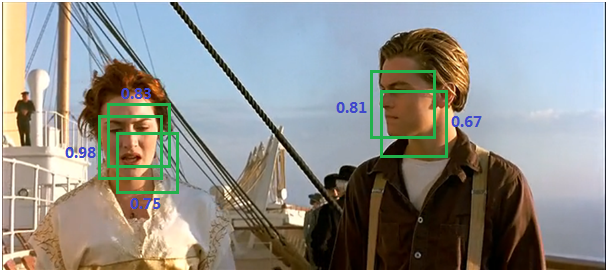
这里我们讨论用于二维图像中目标检测的NMS算法,选取邻域中分数最高的窗。例如在目标检测中,滑动窗经提取特征,经分类器识别后,每个窗都生成一个目标分数(检测到目标的概率)和对应的Bounding Box(对于滑动窗,Bounding Box的大小即为滑动窗大小)。但是滑动窗搜索方法会导致很多Bounding Box与其他Bounding Box存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域中分数最高Bounding Box(是目标的概率最大),并且抑制那些分数低的Bounding Box。
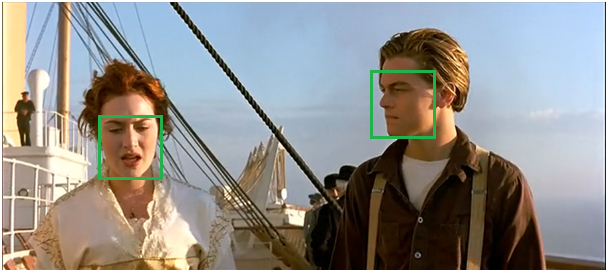
经过NMS后,我们可以看到保留下来了分数最大的框。
NMS原理
简单来说,如下所示:
- 获得Bounding Box列表 B 和其对应的分数 S
- 从 B 中选择具有最大分数的Bounding Box
- 将 从 B 集合中移除并加入最终返回结果 D 中
- 计算其余 Bounding box 与当前最大分数的Bounding box 的IoU,抑制(去除)IoU大于设定阈值的Bounding Box
- 重复以上过程,直至 B 为空,返回 D
常用 IoU 的阈值为 0.3~0.5,关于 IoU 可以参见我的博客。
例子:
有 A,B,C,D,E,F 6个 Box,假设分数依次从小到大,这样NMS的流程如下:
- 选择分数最大的 Bounding Box F,此时 D 中仅有 F
- 判断 A~E 中哪个Bounding Box 和 F 的 IoU 大于阈值。假设 B 和 D 大于,则移除 B 和 D
- 从剩下的 A,C,E 开始,选择分数最大的 E 加入 D 中,同时判断 A 和 C 分别与 E 的 IoU,大于 IoU 阈值则移除。假设没有大于阈值 IoU 的 Box
- 从剩下的 A,C 中选择C,加入 D 中,判断 A 和 C 的 IoU 是否大于阈值。假设大于,则移除A
- 因此,返回的 D 为 [F, E, C]
Python实现
NMS 思想比较简单,算法复杂度为 ,参考代码如下所示[2]:
1 | # import the necessary packages |
还有一个更加快速的 NMS 算法版本[3],使用向量化代码(vectorized code)移除了内部的循环,使用np.maximum和np.minimum函数来代替使用内部for循环来遍历每个单独的 Box————这样可以直接找到array中最大值和最小值。注意np.maximum和np.max的区别。
1 | np.maximum([2, 3, 4], [1, 5, 2]) |
1 | # import the necessary packages |
Soft-NMS
paper: Soft-NMS – Improving Object Detection With One Line of Code
github: soft-nms

如上图所示,之前的 NMS 会出现问题:
- IoU 的阈值如何确定
对于红色 Box 和绿色 Box 是当前的检测结果,二者的得分分别是0.95和0.80。IoU 的阈值设小了会导致,首先选中得分最高的红色 Box ,然后绿色 Box 就会因为与之重叠面积过大而被删掉。 设大了话(应删除的 Box 未被删除),又会容易增大误检,降低检测的精度。
- 两个目标 IoU 过大
因为两个目标的 IoU 过大,即使我们设置一个大的 NMS 的阈值,也可能会导致绿色 Box 被删除。
这时,我们可以想到应该减少目标邻近检测到的 Box 的分数,使得它们的误检率增加的可能性较小,同时在检测的排名列表中又高于明显误检的分数。
解决思路:降低大于 IoU 阈值的 Box 的目标分数,而不是直接删除IoU大于阈值的 Box。
算法
论文中伪代码如下:

如文章题目而言,就是用一行代码来替换掉原来的NMS。但Soft-nms仍需指定一个置信度阈值,然后最后得分大于该阈值的检测框得以保留。
在该算法中,基于重叠部分的大小为相邻检测框设置一个衰减函数而非彻底将其分数置为零。
简单来讲,如果一个检测框与 有大部分重叠,它会有很低的分数;而如果检测框与 M 只有小部分重叠,那么它的原有检测分数不会受太大影响。
具体而言:
传统的NMS处理方法可以通过以下的分数重置函数(Rescoring Function)来表达:
在这个公式中, NMS 采用了硬阈值来判断相邻检测框是否保留。
通过衰减与检测框M有重叠的相邻检测框的检测分数是对NMS算法的一种有效改进,越是与 高度重叠的检测框,越有可能出现误检,它们的分数衰减应该更严重。
论文中soft-nms有两种形式,分别为:
和
对于第一种,当相邻检测框与 M 的重叠度超过重叠阈值 N_t 后,检测框的检测分数呈线性衰减。但是,上述分数重置函数并不是一个连续函数,在重叠程度超过重叠阈值 N_t 时,该分数重置函数产生突变,从而可能导致检测结果序列产生大的变动,因此有了第二种形式。
soft-NMS也是一种贪心算法,并不能保证找到全局最优的检测框分数重置,但其算法复杂度与 NMS 一致,均为 ,并不会带来额外的训练和计算负担。同时,NMS 可以看做是 soft-NMS 采用不连续二值权重函数的一个特例。
在R-FCN以及Faster-RCNN模型中的测试阶段运用Soft-NMS,在MS-COCO数据集上mAP@[0.5:0.95]能够获得大约1%的提升。 如果应用到训练阶段的proposal选取过程理论上也能获得提升。
Reference
[1] N. Bodla, B. Singh, R. Chellappa, and L. S. Davis, “Soft-NMS – Improving Object Detection With One Line of Code,” arXiv:1704.04503 [cs], Apr. 2017.