Introduction

Timsort是一种混合稳定排序算法，源自归并排序（merge sort）和插入排序（insertion sort）。它使用的技术来自于

Peter McIlroy’s “Optimistic Sorting and Information Theoretic Complexity”, in Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 467–474, January 1993.

tim-peters

Tim Peters，图片来自 youtube

2002年Tim Peters为Python编程语言创建了Timsort。自从Python 2.3开始，Timsort一直是Python的标准排序算法。如今，Timsort 已是是 Python、 Java、 Android平台和 GNU Octave 的默认排序算法。

Timsort

概述

Timsort的时间复杂度为 $O(nlgn)$ ，比较一下它与归并排序以及快速排序：

rank

图片来自 bigocheatsheet，里面有常见数据结构操作及排序算法的复杂度比较

Timsort 的运行时间实际与归并排序相似的，本质上利用了归并排序与插入排序，是一种经过优化的归并排序算法。归并排序自身已经到达了比较排序算法时间复杂度的下界，因此优化过的 Timsort 可以认为是目前最快的比较排序算法之一。

思想

现实中的大多数据通常是有部分已经排好序的数据块，Timsort 就利用了这一特点。Timsort 称这些已经排好序的数据块们为 “natural runs”，我们可以将其视为一个一个的“分区”。在排序时，Timsort迭代数据元素，将其放到不同的 run 里，同时针对这些 run ，按规则进行合并至只剩一个，则这个仅剩的 run 即为排好序的结果。

run

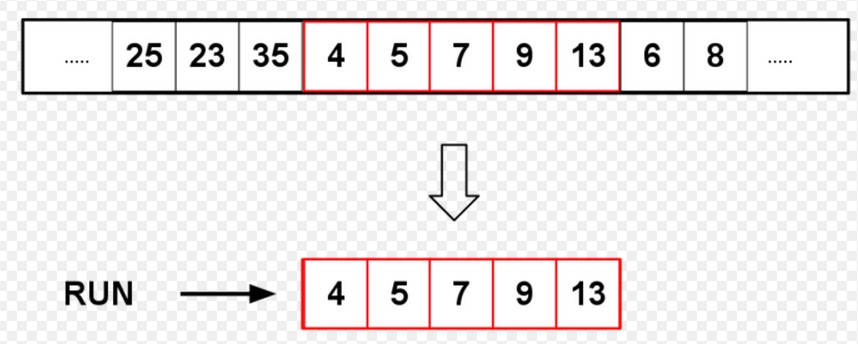
也就是说，Timsort 的大致思想是先采用插入排序将非常小的 run 扩充为较大的 run ，然后再采用归并排序来合并多个 run，所以说 Timsort 实际为归并排序。具体来说，我们需要定义一个参数 minrun ，当 run 长度小于 minrun 时，我们认为它是非常小的 run ，否则认为它是较大的 run 。

综上，Timsort 的过程为：

找到小的 run 扩充为较大的 run
按规则合并 run

下面我们分别描述 Timsort 是如何完成扩充和归并这两个步骤的。

扩充

我们从左到右处理待排序序列，将其划分为若干个 run 。我们从第1个尚未处理的对象开始，找到一个尽可能长的连续严格递减（严格降序）或连续非递减（升序）序列，如果是连续严格递减序列，则可以通过一个简单的“翻转操作”在线性时间内将其变为严格递增序列。

升序: $a[i-1]\leq a[i] \leq a[i+1]$

严格降序: $a[i-1] > a[i] > a[i+1]$

如果这样得到的序列长度等于 minrun ，则我们将其作为一个完整的 run ，继续生成下一 run ；否则我们用插入排序将后面的元素添加进来，直至其长度达到 minrun 为止。我们考虑两个简单的例子：

待排序序列的前4个数是 $3,6,7,5$ ，minrun = 4，则尽可能长的连续非递减序列为 $3,6,7$ ，其长度没有达到4。于是我们将后面的5插入进来，得到长度为4的 run $3,5,6,7$ 。
待排序序列的前4个数是 $9,1,2,7$ ，minrun = 4，则尽可能长的连续递减序列为 $9,1$ ，其长度没有达到4。于是我们依次将后面的2和7插入进来，得到长度为4的 run $1,2,7,9$ 。

如下图所示，如果 run 是依次减小的，我们反转 run （ run 为图中加粗部分）

reverse

合并

我们再来考虑如何合并 run 。

在理想情况下我们应当尽量合并长度相近的 run，这样可以节约计算时间。使用霍夫曼树的归并策略虽然可行，但我们不应该花费太多时间在选择优先合并的 run 上。Timsort 选择了一种折中的方案，它要求最右边的三个 run 的长度尽量满足两个条件。我们记最右边的三个 run 的长度从左到右分别是 $A,B,C$ ，则 Timsort 要求：

$A > B + C$
$B > C$

这样做的目的是让合并后的 run 长度从右至左以指数量级递增，这样我们只需从右至左依次进行合并就可以使每次合并的两个 run 的长度大致相同，实现了平衡。在具体实现上，如果 $A\leq B+C$ ，则我们合并A,B或者 $B,C$ ，这取决于哪一种合并方式生成的新 run 更短。如果 $A>B+C$ 或者 $B\leq C$ ，则我们合并 $B,C$ 。

我们可以每生成一个新的 run 都试图进行合并。在算法结束后，有可能会出现有剩余 run 没有合并的情况。这时我们采用强制合并，直至最终仅剩一个 run ，即排序结果。

我们来看一个具体的例子，考虑待排序序列

$3,6,7,5,3,5,6,2,9,1,2,7,0,9,3,6,0,6,2,6,1,8$

及 minrun = 4，则排序步骤如下所示。其中每一行代表 Timsort 的一个步骤。方块上括号表示在最初生成 run 时首先找到的尽可能长的连续严格递减序列或连续非递减序列，下方括号表示扩充后或者合并的 run 。

$\begin{matrix} \\ 3\; 6\; 7\; 5\; 3\; 5\; 6\; 2\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \overbrace{3\; 6\; 7}\; 5\; 3\; 5\; 6\; 2\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{3\; 5\; 6\; 7}\; 3\; 5; 6\; 2\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{3\; 5\; 6\; 7}\; \overbrace{3\; 5\; 6}\; 2\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{3\; 5\; 6\; 7}\; \underbrace{2\; 3\; 5\; 6}\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; 9\; 1\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; \overbrace{9\; 1}\; 2\; 7\; 0\; 9\; 3\; 6 \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; \underbrace{1\; 2\; 7\; 9}\; 0\; 9\; 3\; 6 \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; \underbrace{1\; 2\; 7\; 9}\; \overbrace{0\; 9}\; 3\; 6 \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; \underbrace{1\; 2\; 7\; 9}\; \underbrace{0\; 3\; 6\; 9} \\ \underbrace{2\; 3\; 3\; 5\; 5\; 6\; 6\; 7}\; \underbrace{0\; 1\; 2\; 3\; 6\; 7\; 9\; 9} \\ \underbrace{0\; 1\; 2\; 2\; 3\; 3\; 3\; 5\; 5\; 6\; 6\; 6\; 7\; 7\; 9\; 9} \end{matrix}$

minrun

最后，我们讨论下 minrun 的选取方式。因此如果待排序序列长度为 minrun，则我们总共会生成 $\lceil \frac{n}{min run } \rceil$ 个初始 run 。

如果 $\lceil \frac{n}{min run } \rceil$ 刚好是2的整数次幂，则归并过程将会非常“完美”，可以表述为一个满二叉树。
如果 $\lceil \frac{n}{min run } \rceil$ 比2的某个整数次幂稍大一点点，则到算法的最后阶段会出现一个超长 run 与一个超短 run 的合并，这是一种非常不好的的情况。

因此，我们会选取 minrun ，使得 $\lceil \frac{n}{min run } \rceil$ 刚好是2的整数次幂或比某个2的整数次幂稍小一点的数。

细节

Python 的 Timsort 的具体说明可以参见 Tim Peters 的说明，非常详尽，也进行了更进一步的优化。

如前所述，run 是已经排好序的一块分区，自然 run 可能会有不同的长度，而 Timesort 根据 run 的长度来选择排序的策略，因此 Timsort也是一个自适应的排序算法。例如，如果 run 的长度小于某一个值，则会选择插入排序算法来排序。

run 的最小长度（minrun）取决于数组的大小。当数组元素少于64个时，那么 run 的最小长度便是数组的长度，这时 Timsort 用插入排序算法来排序。

数组元素小于64个

为了提升速率采用，实际采用的是二分插入排序（binary merge sort) ，这里简单说一下插入排序

插入排序是一种简单的排序，在较大的数组中它很慢，但在小型数组中最为有效，思路如下：

依次访问数组元素
通过将元素插入正确的位置来构建排好序的数组

这个 gif 展示了插入排序的操作过程：

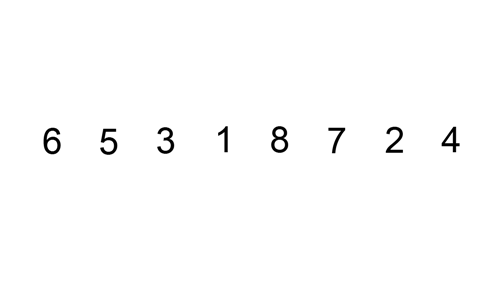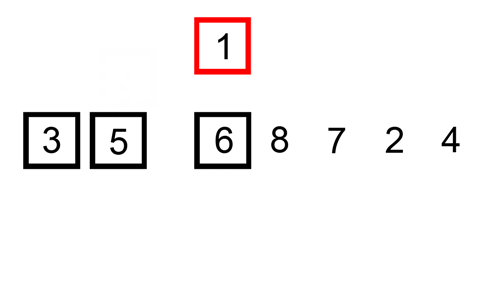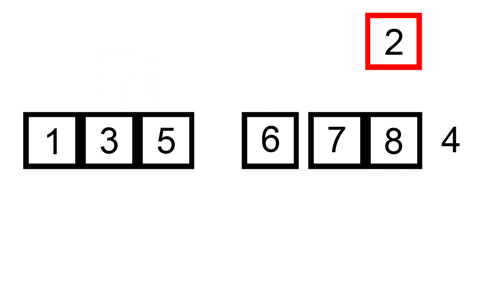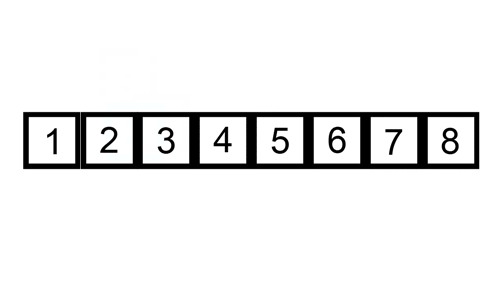
insertion

数组元素大于64个

如果数组大于64个元素，则算法将按照之前的思路开始，首先根据 minrun 查找数组中升序或严格降序的部分，这些部分就是 run 了。

当 Timsort 找到一个 run 时，如果 run 的长度小于 minrun，跟之前一样，我们选择 run 之后的数字插入排序至 run 中，使得 run 的长度到达 minrun。

然后将这个 run 压入栈中，也将该 run 在数组中的起始位置和 run 的长度放入栈中，之后根据先前压入栈中的 run 决定是否该合并 run。

Minimum size (minrun)

如前所述，我们知道当 run 的数目等于或略小于2的幂时，合并两个数组最为有效。所以 Timsort 选择范围为 $[32, 64]$ 的 minrun，使得原始数组的长度除以 minrun 时（ $\lceil \frac{n}{min run } \rceil$ ），等于或略小于2的幂。

具体而言，选择数组长度的六个最高标志位，如果其余的标志位被设置，则加1：

189：10111101，取前六个最高标志位为101111(47)，同时最后两位为01，所以 minrun 为47+1， $\lceil \frac{n}{min run } \rceil=4$ 满足要求。
976：11 1101 0000，取前六个最高标志位为111101(61)，同时最后几位为0000，所以 minrun 为61， $\lceil \frac{n}{min run } \rceil=16$ 满足要求。

Merging

合并的时候，按照思路中的规则进行合并，满足以下条件时，合并结束：

$X>Y+Z$
$Y>Z$

例如：如果 $X<Y+Z$ ，那么 $X+Y$ 合并为一个新的 run，然后入栈。重复上述步骤，直到同时满足上述2个条件。

当合并结束后，Timsort 会继续找下一 run，然后找到以后入栈，重复上述步骤，即每次 run 入栈都会检查是否需要合并2个 run。

注意到，我们只在栈的顶部进行这样的合并，这个配合 run 是升序或严格降序的可以保证 Timsort 是稳定的，如下图所示。

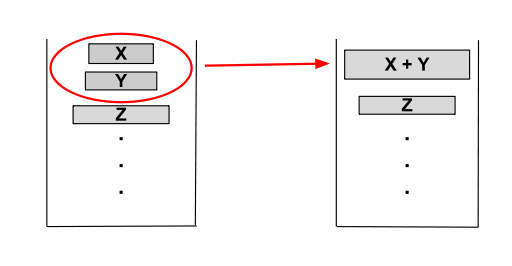
merge

Timsort 并没执行原址(in_place)的归并，因为保证原址并稳定的话，需要很大的开销。

实际中 Timsort 合并2个相邻的 run 需要临时存储空闲，临时存储空间的大小是2个 run 中较小的 run 的大小。Timsort算法先将较小的 run 复制到这个临时存储空间，然后用原先存储这2个 run 的空间来存储合并后的 run。

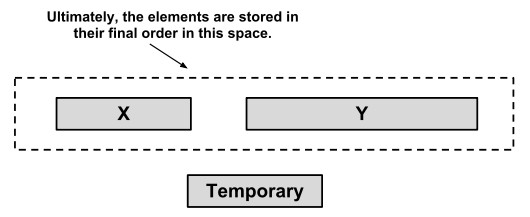
temporary

合并算法是用简单插入排序，依次从左到右或从右到左比较，然后合并2个 run。

为了提高效率，Timsort用二分插入排序（binary merge sort）。即先用二分查找（binary search）找到插入的位置，然后再插入。

Galloping mode

在 Galloping mode 中，算法在一个 run 中搜索另一个 run 的第一个元素。通过将该初始元素与另一个 run 的第 $2k-1$ 个元素（即1,3,5…）进行比较来完成的，以便获得初始元素所在的元素范围。这缩短了二分查找的范围，从而提高了效率。如果发现 Galloping 的效率低于二分查找，则退出 Galloping mode。

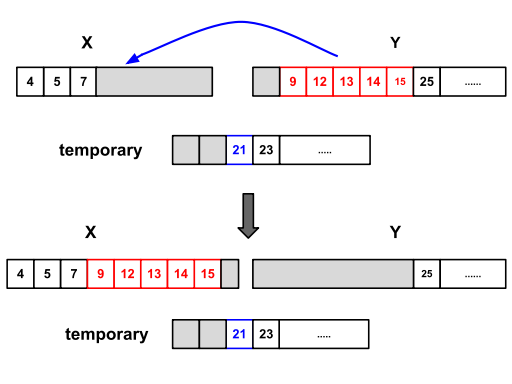
例如，我们要将 X 和 Y 这2个 run 合并，且X是较小的 run，以及 X 和 Y 已经分别是排好序的，如下图所示。

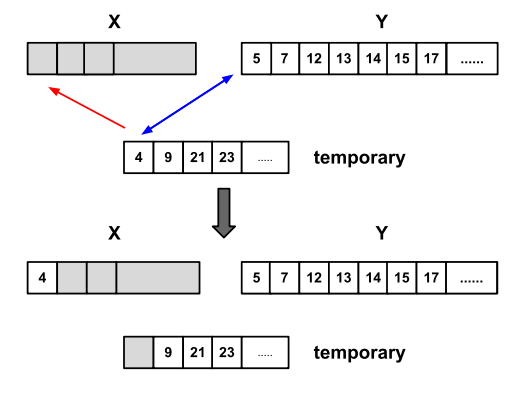
merging-xy1

二分查找会找到 X 中第一个大于 Y[0] 的元素 x，当找到 x 时，可以在合并时忽略 x 之前的元素。类似的，还可以在 Y 中找到第一个大于 X[-1] 的元素 y，当找到 y 时，可以在合并时忽略 y 之后的元素，这种查找可能在随机数中效率不会很高，但是在其他情况下有很高的效率。

merging-xy2

当算法到达最小阈值min_gallop时，算法切换到 Galloping mode，试图利用数据中的那些可以直接排序的元素。只有当一个 run 的初始元素不是另一个 run 的前七个元素之一时，Galloping 才有用。这意味着初始阈值为7。

为了避免 Galloping mode 的缺点，合并函数会调整阈值。如果所选元素来自先前返回元素的同一数组，则min_gallop减1。否则，该值增加1，从而阻止返回到 Galloping mode 。在随机数据的情况下，min_gallop的值会变得非常大，以至于 Galloping mode 永远不会再次发生。

Galloping 并不总是有效的。在某些情况下，Galloping mode 会有比简单的线性搜索更多的比较。

分析

本质上 Timsort 是一个经过大量优化的归并排序，而归并排序已经到达了最坏情况下，比较排序算法时间复杂度的下界，所以在最坏的情况下，Timsort 时间复杂度为 $O(nlgn)$ 。在最佳情况下，即输入已经排好序，它则以线性时间运行 $O(n)$ 。

Code

此代码来自于 here。

虽然这个代码不完整，也不类似于Python的官方sorted()源码，但是已经可以获得 Timsort 的总体感觉。如果你想看到 Timsort 的官方原始代码，参见此处（是用C语言实现的，而不是Python）。

# based off of this code https://gist.github.com/nandajavarma/a3a6b62f34e74ec4c31674934327bbd3
# Brandon Skerritt
# https://skerritt.tech

def binary_search(the_array, item, start, end):
    if start == end:
        if the_array[start] > item:
            return start
        else:
            return start + 1
    if start > end:
        return start

    mid = round((start + end)/ 2)

    if the_array[mid] < item:
        return binary_search(the_array, item, mid + 1, end)

    elif the_array[mid] > item:
        return binary_search(the_array, item, start, mid - 1)

    else:
        return mid

"""
Insertion sort that timsort uses if the array size is small or if
the size of the "run" is small
"""
def insertion_sort(the_array):
    l = len(the_array)
    for index in range(1, l):
        value = the_array[index]
        pos = binary_search(the_array, value, 0, index - 1)
        the_array = the_array[:pos] + [value] + the_array[pos:index] + the_array[index+1:]
    return the_array

def merge(left, right):
    """Takes two sorted lists and returns a single sorted list by comparing the
    elements one at a time.
    [1, 2, 3, 4, 5, 6]
    """
    if not left:
        return right
    if not right:
        return left
    if left[0] < right[0]:
        return [left[0]] + merge(left[1:], right)
    return [right[0]] + merge(left, right[1:])

def timsort(the_array):
    runs, sorted_runs = [], []
    length = len(the_array)
    new_run = [the_array[0]]

    # for every i in the range of 1 to length of array
    for i in range(1, length):
        # if i is at the end of the list
        if i == length - 1:
            new_run.append(the_array[i])
            runs.append(new_run)
            break
        # if the i'th element of the array is less than the one before it
        if the_array[i] < the_array[i-1]:
            # if new_run is set to None (NULL)
            if not new_run:
                runs.append([the_array[i]])
                new_run.append(the_array[i])
            else:
                runs.append(new_run)
                new_run = []
        # else if its equal to or more than
        else:
            new_run.append(the_array[i])

    # for every item in runs, append it using insertion sort
    for item in runs:
        sorted_runs.append(insertion_sort(item))
    
    # for every run in sorted_runs, merge them
    sorted_array = []
    for run in sorted_runs:
        sorted_array = merge(sorted_array, run)

    print(sorted_array)

timsort([2, 3, 1, 5, 6, 7])

Reference

Timsort — the fastest sorting algorithm you’ve never heard of
算法笔记——刁瑞 / 谢妍
Timsort – Wiki
Nicolas Auger, Cyril Nicaud, Carine Pivoteau. Merge Strategies: from Merge Sort to TimSort. 2015.

Timsort原理学习

目录