曲线拟合用于查找一系列数据点的“最佳拟合”线或曲线。 大多数情况下,曲线拟合将产生一个函数,可用于在曲线的任何位置找到点。 在某些情况下,也可能不关心找到函数,而是只想使用曲线拟合来平滑数据并改善绘图的外观。
简而言之,曲线拟合就是在受到一定约束条件的情况下,构建可以表示一系列数据点的曲线或数学函数的过程。更加数学化一点的话,对于一个给定的数据集,曲线拟合是以方程形式引入因变量和自变量之间的数学关系的过程。
一般来说,曲线拟合可以认为有以下形式:
平滑
我们使用一个函数来尽可能的表示(即逼近)数据集中点的数据。
逼近
或者如前文所述,我们只想使用曲线拟合来平滑数据并改善绘图的外观。前两种情况下,数据的一般会有相当程度的误差或噪声。
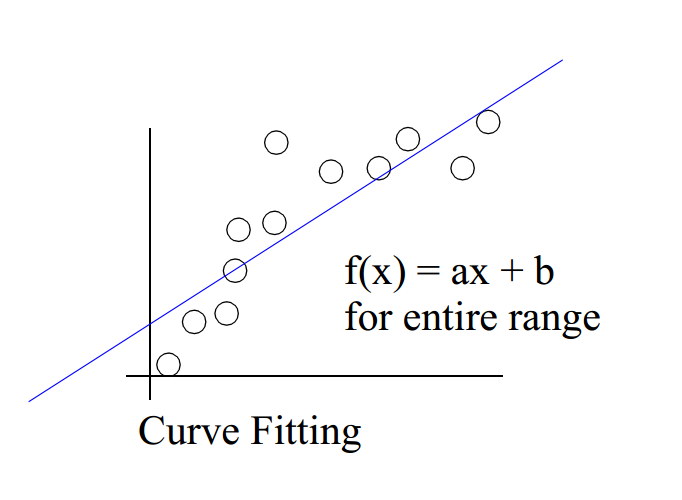
如下所示,为线性拟合:
插值
对于给定的数据集,产生一个或多个插值曲线通过数据集的每一个点。这种情况下,我们认为数据点很足够准确的。
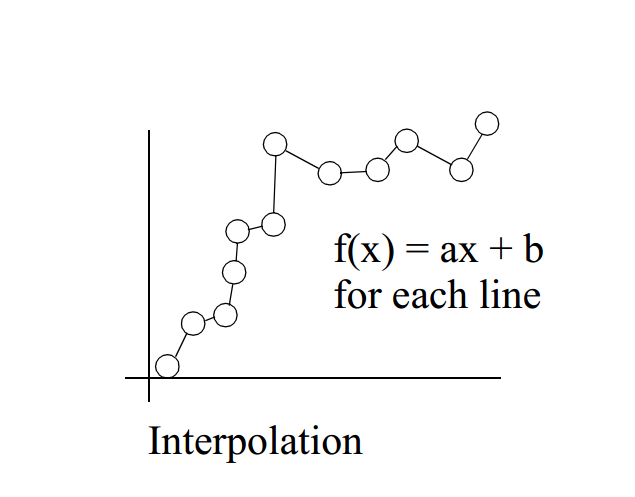
如图所示,为线性插值:
这里我们主要讲述在一定约束条件下,如何用一个函数尽可能的表示(即逼近)数据集中的点。同时,使用基于最小二乘的多项式曲线来拟合数据点。
多项式曲线即为用多项式函数表示的曲线:
f ( x ) = a n ∗ x n + a n − 1 ∗ x n − 1 + ⋅ ⋅ ⋅ + a 2 ∗ x 2 + a 1 ∗ x + a 0 f(x)=a_n*x^n+a_{n-1}*x^{n-1}+···+a_2*x^2+a_1*x+a_0
f ( x ) = a n ∗ x n + a n − 1 ∗ x n − 1 + ⋅ ⋅ ⋅ + a 2 ∗ x 2 + a 1 ∗ x + a 0
f ( x ) = ∑ i = 0 n a i ∗ x i f(x)=\sum_{i=0}^{n}{a_i*x^i}
f ( x ) = i = 0 ∑ n a i ∗ x i
其中n n n
当n n n y = a ∗ x + b y=a*x+b y = a ∗ x + b n n n n n n
这样对于数据集中的n n n ( x , y ) (x,y) ( x , y )
{ y 1 ^ ( x , w ) = w 0 + w 1 ∗ x 1 + w 2 ∗ x 1 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x 1 m − 1 + w m ∗ x 1 m y 2 ^ ( x , w ) = w 0 + w 1 ∗ x 2 + w 2 ∗ x 2 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x 2 m − 1 + w m ∗ x 2 m ⋮ y n − 1 ^ ( x , w ) = w 0 + w 1 ∗ x n − 1 + w 2 ∗ x n − 1 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x n − 1 m − 1 + w m ∗ x n − 1 m y n ^ ( x , w ) = w 0 + w 1 ∗ x n + w 2 ∗ x n 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x n m − 1 + w m ∗ x n m \left\{\begin{matrix} \hat{y_1}(x,w)=w_0+w_1*x_1+w_2*x_1^2+···+w_{m-1}*x_1^{m-1}+w_m*x_1^m
\\ \hat{y_2}(x,w)=w_0+w_1*x_2+w_2*x_2^2+···+w_{m-1}*x_2^{m-1}+w_m*x_2^m
\\ \vdots
\\ \hat{y_{n-1}}(x,w)=w_0+w_1*x_{n-1}+w_2*x_{n-1}^2+···+w_{m-1}*x_{n-1}^{m-1}+w_m*x_{n-1}^m
\\ \hat{y_n}(x,w)=w_0+w_1*x_n+w_2*x_n^2+···+w_{m-1}*x_n^{m-1}+w_m*x_n^m
\end{matrix}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ y 1 ^ ( x , w ) = w 0 + w 1 ∗ x 1 + w 2 ∗ x 1 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x 1 m − 1 + w m ∗ x 1 m y 2 ^ ( x , w ) = w 0 + w 1 ∗ x 2 + w 2 ∗ x 2 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x 2 m − 1 + w m ∗ x 2 m ⋮ y n − 1 ^ ( x , w ) = w 0 + w 1 ∗ x n − 1 + w 2 ∗ x n − 1 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x n − 1 m − 1 + w m ∗ x n − 1 m y n ^ ( x , w ) = w 0 + w 1 ∗ x n + w 2 ∗ x n 2 + ⋅ ⋅ ⋅ + w m − 1 ∗ x n m − 1 + w m ∗ x n m
将其写为矩阵形式:
Y ^ = X W \hat{Y}=XW
Y ^ = X W
其中,W= (w_0,w_1,w_2,···,w_{m-1},w_m)^T,为( m + 1 ) × 1 (m+1)\times 1 ( m + 1 ) × 1 X X X n × ( m + 1 ) n\times (m+1) n × ( m + 1 )
X = [ 1 1 1 ⋯ 1 x 1 x 2 x 3 ⋯ x n ⋮ ⋮ ⋮ ⋮ ⋮ x 1 m x 2 m x 3 m ⋯ x n m ] T X=\begin{bmatrix}
1 & 1 & 1 & \cdots & 1\\
x_1 & x_2 & x_3 & \cdots & x_n \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
x_1^m & x_2^m & x_3^m & \cdots & x_n^m
\end{bmatrix}^T
X = ⎣ ⎢ ⎢ ⎡ 1 x 1 ⋮ x 1 m 1 x 2 ⋮ x 2 m 1 x 3 ⋮ x 3 m ⋯ ⋯ ⋮ ⋯ 1 x n ⋮ x n m ⎦ ⎥ ⎥ ⎤ T
自然,我们可以看到随着m m m d e g r e e degree d e g r e e
实际上,我们可以发现多项式曲线拟合所使用的多项式模型,是一个针对非线性函数数据的线性模型。
这样,多项式曲线拟合即可表示为,给定数据集,求近似曲线f ( x ) f(x) f ( x ) y y y
有了模型,这下我们使用最小二乘法来求解W W W
对于矩阵方程:A x = b Ax=b A x = b b ∈ R m × 1 b\in R^{m\times 1} b ∈ R m × 1 A ∈ R m × n A\in R^{m\times n} A ∈ R m × n
超定方程 m > n m>n m > n A A A b b b
盲矩阵方程 均b b b A A A
欠定方程 m < n m<n m < n A A A b b b x x x
最小二乘法,是最常用的线性参数估计方法,常用于对平面上的点拟合直线,对高维空间的点拟合超平面。
考虑超定矩阵方程A x = b Ax=b A x = b b ∈ R m × 1 b\in R^{m\times 1} b ∈ R m × 1 A ∈ R m × n A\in R^{m\times n} A ∈ R m × n m > n m>n m > n
假定b b b b = b 0 + e b=b_0+e b = b 0 + e b 0 b_0 b 0 e e e
为了抵消误差对矩阵方程的求解的影响,我们引入一校正向量Δ b \Delta b Δ b b + Δ b = b 0 + e + Δ b → b 0 b+\Delta b=b_0+e+\Delta b\rightarrow b_0 b + Δ b = b 0 + e + Δ b → b 0
A x = b + Δ b ⇒ A x = b 0 Ax=b+\Delta b\Rightarrow Ax=b_0
A x = b + Δ b ⇒ A x = b 0
的转换。也就是说,选择校正向量Δ b = A x − b \Delta b=Ax-b Δ b = A x − b A x = b 0 Ax=b_0 A x = b 0
矩阵方程的这一求解思想可以用下面的优化问题描述
m i n x ∣ ∣ Δ b ∣ ∣ 2 = ∣ ∣ A x − b ∣ ∣ 2 2 = ( A x − b ) T ( A x − b ) \mathop{min}_x ||\Delta b||^2=||Ax-b||^2_2=(Ax-b)^T(Ax-b)
m i n x ∣ ∣ Δ b ∣ ∣ 2 = ∣ ∣ A x − b ∣ ∣ 2 2 = ( A x − b ) T ( A x − b )
这一方法被称为普通最小二乘(Ordinary least squares, OLS)法,一般称为最小二乘法。
于是,矩阵方程的A x = b Ax=b A x = b
x ^ L S = a r g m i n x ∣ ∣ A x − b ∣ ∣ 2 2 \hat{x}_{LS}=arg\mathop{min}_x||Ax-b||^2_2
x ^ L S = a r g m i n x ∣ ∣ A x − b ∣ ∣ 2 2
展开ϕ = ( A x − b ) T ( A x − b ) \phi =(Ax-b)^T(Ax-b) ϕ = ( A x − b ) T ( A x − b )
ϕ = x T A T A x − x T A T b − b T A x + b T b \phi = x^TA^TAx-x^TA^Tb-b^TAx+b^Tb
ϕ = x T A T A x − x T A T b − b T A x + b T b
求ϕ \phi ϕ x x x
d ϕ d x = 2 A T A x − 2 A T b = 0 \frac{d\phi}{dx}=2A^TAx-2A^Tb=0
d x d ϕ = 2 A T A x − 2 A T b = 0
也就是说,x x x
A T A x = A T b A^TAx=A^Tb
A T A x = A T b
当矩阵A m × n A_{m\times n} A m × n
超定方程(m > n m>n m > n r a n k ( A ) = n rank(A)=n r a n k ( A ) = n
由于A T A A^TA A T A
x L S = ( A T A ) − 1 A T b x_{LS}=(A^TA)^{-1}A^Tb
x L S = ( A T A ) − 1 A T b
对于不满秩(r a n k ( A ) < n rank(A)<n r a n k ( A ) < n
x L S = ( A T A ) † A T b x_{LS}=(A^TA)^\dagger A^Tb
x L S = ( A T A ) † A T b
其中† \dagger †
在参数估计理论,称参数向量θ \theta θ θ ^ \hat{\theta} θ ^ E { θ ^ } = θ E\{\hat{\theta}\}=\theta E { θ ^ } = θ θ ^ \hat{\theta} θ ^
在统计学中,高斯-马尔可夫定理(Gauss-Markov Theorem)陈述的是:在线性回归模型中,如果误差满足零均值、同方差且互不相关 ,则回归系数的最佳线性无偏估计(BLUE, Best Linear unbiased estimator)就是 普通最小二乘法估计 。
这里最佳的意思是指相较于其他估计量有更小方差的估计量,同时把对估计量的寻找限制在所有可能的线性无偏估计量中。
值得注意的是这里不需要假定误差满足独立同分布(iid)或正态分布,而仅需要满足零均值 、不相关 及同方差 这三个稍弱的条件。
关于Gauss-Markov定理更详细内容见此:Wiki
放入最小二乘法中,对于数据向量b b b A x = b 0 + e Ax=b_0+e A x = b 0 + e e e e
E\{e\}=0 \\
Cov\{e\}=E\{ee^T\}=\sigma^2I \\
当且仅当r a n k ( A ) = n rank(A)=n r a n k ( A ) = n x x x x ^ \hat{x} x ^
也就是说当e e e e e e σ 2 \sigma^2 σ 2
若加性误差向量e = [ e 1 , ⋅ ⋅ ⋅ e m ] T e=[e_1,···e_m]^T e = [ e 1 , ⋅ ⋅ ⋅ e m ] T
f ( e ) = 1 π m ∣ Γ e ∣ e x p [ − ( e − μ e ) T Γ e − 1 ( e − μ e ) ] f(e)=\frac{1}{\pi^m|\Gamma_e|}exp[-(e-\mu_e)^T{\Gamma_e}^{-1}(e-\mu_e)]
f ( e ) = π m ∣ Γ e ∣ 1 e x p [ − ( e − μ e ) T Γ e − 1 ( e − μ e ) ]
其中,∣ Γ e ∣ |\Gamma_e| ∣ Γ e ∣ Γ e = d i a g ( σ 1 2 , ⋅ ⋅ ⋅ , σ m 2 ) \Gamma_e=diag(\sigma_1^2,···,\sigma^2_m) Γ e = d i a g ( σ 1 2 , ⋅ ⋅ ⋅ , σ m 2 )
在Gauss-Markov定理条件下(即误差向量e e e σ 2 \sigma^2 σ 2 e e e
f ( e ) = 1 ( π σ 2 ) m e x p ( − 1 σ 2 e T e ) = 1 ( π σ 2 ) m e x p ( − 1 σ 2 ∣ ∣ e ∣ ∣ 2 2 ) f(e)=\frac{1}{(\pi\sigma^2)^m}exp(-\frac{1}{\sigma^2}e^Te)=\frac{1}{(\pi\sigma^2)^m}exp(-\frac{1}{\sigma^2}||e||^2_2)
f ( e ) = ( π σ 2 ) m 1 e x p ( − σ 2 1 e T e ) = ( π σ 2 ) m 1 e x p ( − σ 2 1 ∣ ∣ e ∣ ∣ 2 2 )
其似然函数为
L ( e ) = l o g f ( e ) = − 1 π m σ 2 ( m + 1 ) ∣ ∣ e ∣ ∣ 2 2 = − 1 π m σ 2 ( m + 1 ) ∣ ∣ A x − b ∣ ∣ 2 2 L(e)=logf(e)=-\frac{1}{\pi^m\sigma^{2(m+1)}||e||^2_2}=-\frac{1}{\pi^m\sigma^{2(m+1)}}||Ax-b||^2_2
L ( e ) = l o g f ( e ) = − π m σ 2 ( m + 1 ) ∣ ∣ e ∣ ∣ 2 2 1 = − π m σ 2 ( m + 1 ) 1 ∣ ∣ A x − b ∣ ∣ 2 2
于是,A x = b Ax=b A x = b
x ^ = a r g m a x x − 1 π m σ 2 ( m + 1 ) ∣ ∣ A x − b ∣ ∣ 2 2 = a r g m i n x 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 = x ^ L S \hat{x}=arg \mathop{max}_{x}\frac{-1}{\pi^m\sigma^{2(m+1)}}||Ax-b||^2_2=arg\mathop{min}_x\frac{1}{2}||Ax-b||^2_2=\hat{x}_{LS}
x ^ = a r g m a x x π m σ 2 ( m + 1 ) − 1 ∣ ∣ A x − b ∣ ∣ 2 2 = a r g m i n x 2 1 ∣ ∣ A x − b ∣ ∣ 2 2 = x ^ L S
也就是说,在Guass-Markov定理的条件下,矩阵方程A x = b Ax=b A x = b
Python的numpy模块已经实现了很多数值函数,自然也包括了最小二乘法numpy.linalg.lstsq,并且numpy将其封装成了polyfit函数,然后配合poly1d函数,即可完成基于最小二乘法的多项式曲线拟合。
但是在这里为了学习最小二乘法,我使用Python实现了一个简单的最小二乘法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 def leastSquares (X, Y, degree) : Xs = [] for i in range(degree+1 ): Xs.append(X**i) Xs = np.array(Xs).T Y = Y.T XT = Xs.transpose() W = np.dot(np.dot(np.linalg.inv(np.dot(XT,Xs)),XT),Y) return W[::-1 ] x = np.arange(1 , 17 , 1 ) y = np.array([4.00 , 6.40 , 8.00 , 8.80 , 9.22 , 9.50 , 9.70 , 9.86 , 10.00 , 10.20 , 10.32 , 10.42 , 10.50 , 10.55 , 10.58 , 10.60 ]) print(leastSquares(x, y, 3 ))
1 [ 0.00624491 -0.20371114 2.18193147 2.57208791 ]
然后使用numpy中的polyfit,我们可以得到一致的结果,说明实现的是正确的,但是缺少很多优化,和numpy中的实现相比速度很慢。
1 2 >>> print(np.polyfit(x, y, 3 ))>>> [ 0.00624491 -0.20371114 2.18193147 2.57208791 ]
最后,我们使用多项式曲线拟合我们的数据,阶数越高,模型参数更多就可以表示更加复杂的数据:
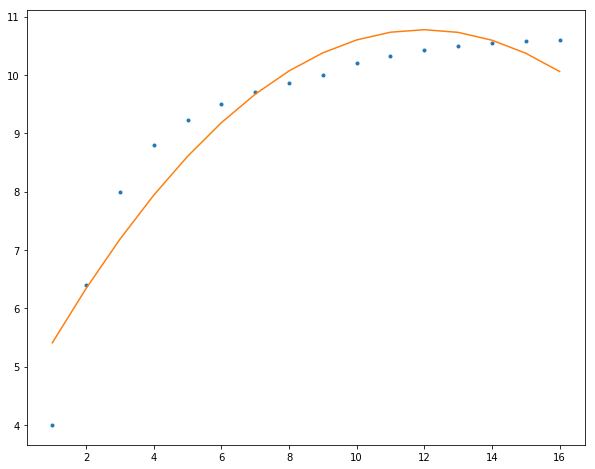
2阶
1 2 3 4 5 6 7 8 f = np.polyfit(x, y, 2 ) p = np.poly1d(f) yvals = p(x) plt.figure(figsize=(10 ,8 )) plt.plot(x, y, '.' ) plt.plot(x, yvals) plt.show()
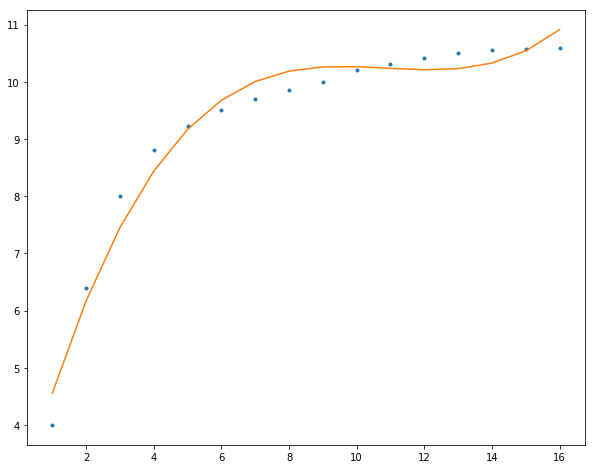
3阶
4阶