Python代码：GitHub

​ 一般意义上讲，一个社区也可以被称为群、聚类或模块，是网络中一群阶段或边的集合，其内部的节点间连接较为紧密，而社区间的连接却相对稀疏。之前实现了针对无权网络的GN算法，这篇文章则是针对加权网络的GN算法

​ 针对无权网络的GN算法，可以看一看我之前的那篇文章

针对加权网络的GN算法

GN算法

GN算法是一种利用基于边介数的社区发现算法

这样的社区发现算法的主要思路为：计算网络中所有边的边介数，然后寻找边介数值最大的边并移除。在移除时，会改变一些边的边介数。以前经过被移除边的最短路径，现在改为经由其他边，因此必须重新计算边介数，然后再次搜索值最大的边并移除，依此类推。当一条接一条边被移除时，最初连通的网络最终会被分成两部分、三部分等等，直至网络的每一个成为一个社区，是一种分裂算法。

算法的执行过程可用树状图表示，如下图所示。算法从顶部开始生成树状图，首先是单个连通网络，然后将其不断划分，直至每个分支只有单个结点为止。在算法运行期间，每个独立的网络结构状态对应于树状图的水平切分，在图2中用红线表示。与红线相交的每个分支代表一组节点，即一个社区，沿分支向下到底部的全部节点都为其成员。因此对于一个连通网络，树状图能够得到算法执行全过程中每个阶段里网络划分的社区结构。

1

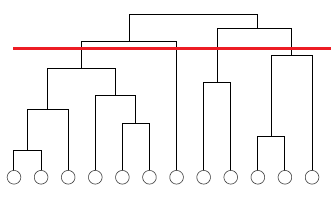
针对加权网络的GN算法描述

这里给出针对有权网络的Girvan-Newman算法，加权Girvan-Newman算法求解的具体实现过程为:

  1. 忽略边的权重，以无权网络计算网络中所有连接边的边介数；
  2. 将边介数除以对应边的权重得到边权比；
  3. 找到边权比最高的边将它移除，并计算网络的模块性 Q 函数，在计算中当边权比最高的边有多条时，同时移除这些边，并将此时移除的边和Q值进行存储；
  4. 重复步骤1，2，直到网络中所有的边均被移除。
  5. Girvan-Newman算法划分结束后，取出Q值最大时的序号，在原始矩阵中依次去除截止到该次划分的边。得出最终连通矩阵，矩阵的值为权值。

Python实现

Python代码：GitHub

Python环境需求

这里使用Python的 NetworkX 包以及 Matplotlib 包来完成对于Girvan-Newman算法的演示

以及Gephi，一个基于JVM的可视化平台。

NetworkX是一个用于创建，操作和研究复杂网络的结构、动态和功能的Python包

Matplotlib是一个Python 2D绘图库，利用它完成模块化函数Q与划分社团数目的关系曲线，之后使用Gephi作为网络的可视化工具，将GML文件中的图中划分的社团表示出来。

Python环境需求：

  • Python-3.6.3
  • NetworkX-2.0
  • Matplotlib-2.1.0

Lesmiserables 网络

Lesmiserables网络是维克多·雨果所著《悲惨世界》（Les Misérables）一书中人物角色间的加权连接网络。一共有77个节点，254条边，也并不知道应划分的社团数量。

2

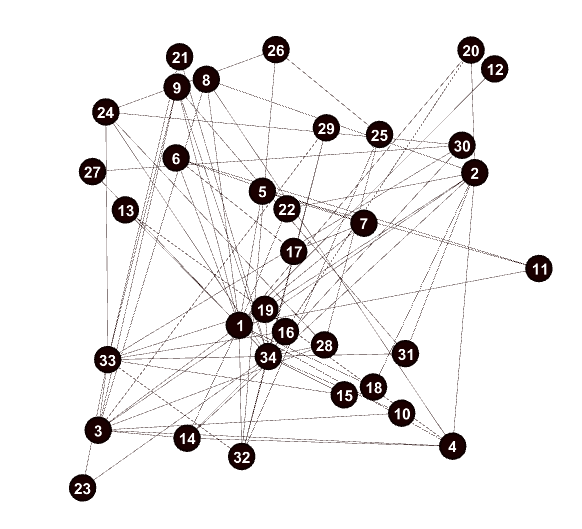
运行完毕 Girvan-Newman_weighted.py 我们可以得到以下结果，Q值在划分社团数为20时，达到最大值，如下图所示。当然我们也可以采用Q值与划分社区数量曲线中的极大值点，作为划分社团的依据。

3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
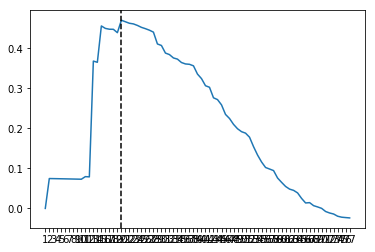
-------------------------------------theMax Q and divided communities---------------------------------------

Thenumber of Communites: 20

Communites:[

['Myriel','MlleBaptistine', 'MmeMagloire', 'CountessDeLo', 'Count', 'OldMan','Champtercier', 'Cravatte', 'Geborand', 'Napoleon'],

['Labarre'],

['Anzelma','Montparnasse', 'Gueulemer', 'Claquesous', 'MotherInnocent', 'Eponine','Babet', 'Fauchelevent', 'Woman2', 'MlleGillenormand', 'Marius','MmeThenardier', 'Brujon', 'Woman1', 'Thenardier', 'Javert', 'Gillenormand','Simplice', 'Valjean', 'Cosette'], ['Listolier', 'Tholomyes', 'Dahlia','Blacheville', 'Fameuil', 'Favourite', 'Zephine', 'Marguerite', 'Fantine'], 

['MmeDeR'], 

['Isabeau'], 

['Gervais'],

['Brevet','Cochepaille', 'Judge', 'Champmathieu', 'Bamatabois', 'Chenildieu'], 

['Perpetue'],['Scaufflaire'],

['MmePontmercy','Pontmercy'],

['Boulatruelle'],

['Gribier'], 

['Jondrette'],

['Enjolras', 'Joly','Child1', 'Grantaire', 'Courfeyrac', 'MmeHucheloup', 'MotherPlutarch','Feuilly', 'Bahorel', 'Mabeuf', 'Combeferre', 'MmeBurgon', 'Prouvaire','Child2', 'Gavroche', 'Bossuet'], 

['Magnon'],

['MlleVaubois'], 

['LtGillenormand'], 

['BaronessT'], 

['Toussaint']]

Max_Q: 0.4701546903093807

将输出的结果导入到Gephi后，以group为依据着色，可得到下图，我们发现Girvan-Newman算法对带权值网络也是比较有效的。

4

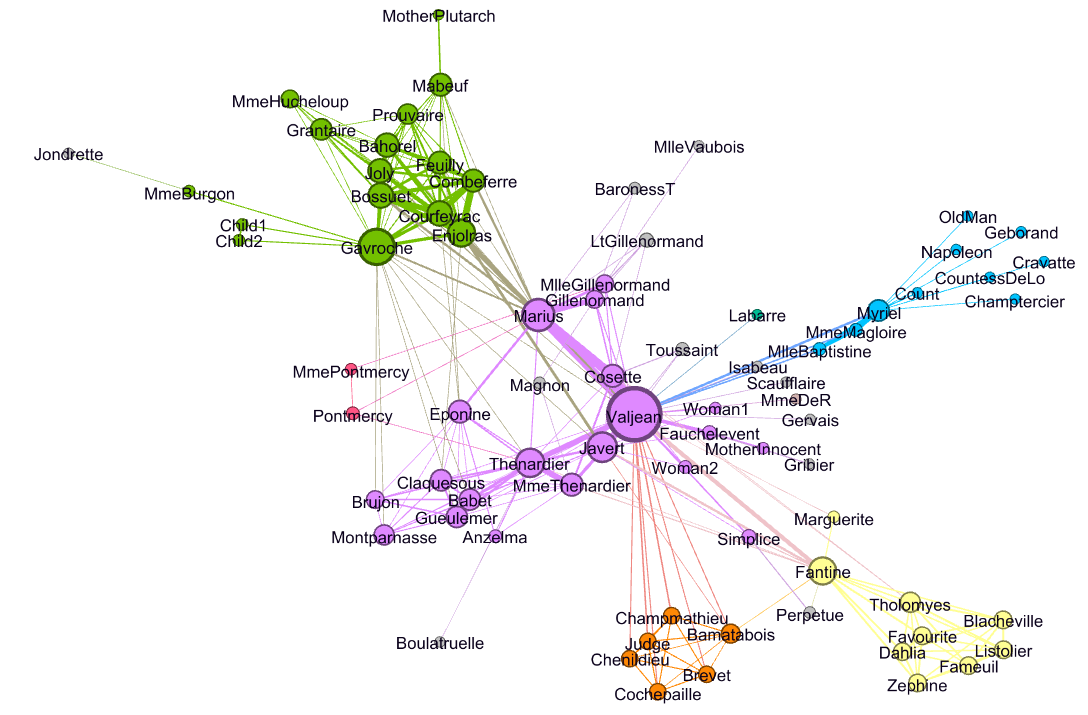
Girvan-Newman算法分析

对于mm条边和nn个节点的网络，Girvan-Newman算法计算边介数的时间复杂度为O(n(m+n))O(n(m+n))，且在移除mm条边的每条边前都需要执行该计算，所以整个算法的时间复杂度为O(mn(m+n))O(mn(m+n))。

若在m∝nm∝n稀疏网络中的时间复杂度为O(n3)O(n^3 )。

这里总结下Girvan-Newman算法的优缺点。

Girvan-Newman算法的优点：

  1. 在知道划分社团数量时，可以较为精确的给出社团的划分结果；

  2. 可以给出不同程度的社团划分结果，可以揭示关于网络层次结构的信息；

Girvan-Newman算法的缺点：

  1. 在计算边介数的时候可能会有很多重复计算最短路径的情况，时间复杂度太高；
  2. 若无法知道应该划分社团的数量，算法效果会相对较差；

总而言之，Girvan-Newman算法不必依赖多余的信息来判断得到的社团结构是否具有实际意义,而是可以直接从网络的拓扑结构来进行分析。

但是该算法的耗时比较大，时间复杂度为O(mn(m+n))O(mn(m+n))，因此它仅仅适用于中等规模的复杂网络(n≤10000)(n≤10000)。