介绍

filtering 滤波

关于filtering 滤波我觉得知乎上的这个回答非常的精彩，我个人觉得用加权平均来理解，更好一些

一位专业课的教授给我们上课的时候，曾谈到：filtering is weighting（滤波即加权）。

滤波的作用就是给不同的信号分量不同的权重。最简单的loss pass filter， 就是直接把低频的信号给 1 权重，而给高频部分 0 权重。对于更复杂的滤波，比如维纳滤波, 则要根据信号的统计知识来设计权重。

从统计信号处理的角度，降噪，可以看成滤波的一种。降噪的目的在于突出信号本身而抑制噪声影响。从这个角度，降噪就是给信号一个高的权重而给噪声一个低的权重。维纳滤波就是一个典型的降噪滤波器。

​ 引自知乎：王航臣 https://www.zhihu.com/question/34809533/answer/61345742

同时插值、滤波、预测可以理解为：

插值 interpolation（或者说平滑 smoothing），就是用 过去 的数据来拟合 过去 的数据，比如牛顿插值，拉格朗日插值
滤波 filtering，是用 当前 和 过去 的数据来求取 当前 的数据
预测 prediction，是指用 当前 和 过去 的数据来求取 未来 的数据

关于 Kalman Filter

Kalman Filter 算法，是一种递推预测滤波算法，算法中即涉及到滤波，也涉及到对下一时刻数据的预测。Kalman Filter 由一系列递归数学公式描述。它们提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质。

Kalman Filter 也可以被认为是一种数据融合算法（Data fused algorithm），已有50多年的历史，是当今使用最重要和最常见的数据融合算法之一。Kalman Filter 的巨大成功归功于其小的计算需求，优雅的递归属性以及作为具有高斯误差统计的一维线性系统的最优估计器的状态[1]。

Kalman Filter 只能减小均值为0的测量噪声带来的影响。只要噪声期望为0，那么不管方差多大，只要迭代次数足够多，那效果都很好。反之，噪声期望不为0，那么估计值就还是与实际值有偏差。

因此使用 Kalman Filter 不用假设误差是正态分布，不过若所有的误差都是正态分布，Kalman Filter 可以得到正确的条件概率估计。关于此，可以参见文章[3]。

图形解释

这里主要参考了文章[1] 和知乎的回答[4]。

让我们考虑一个一维问题，也是一个最简单的情况，一个在轨道上的小车的运动情况。

假若我们知道了小车的运动方向、所受的力、质量等等参数，以及初始状态，理论上我们可以求出它任意时刻的状态。当然，实际情况不会这么美好：

这个推算的过程可能会受到各种不确定因素的影响（内在的外在的，比如刮风下雨地震，小车结构不紧密，轮子不圆等等）导致我们并不能精确标识小车实际的状态。

假设每个状态分量受到的不确定因素都服从正态分布：

对小车的位置进行估计

下图：t=0 时小车的位置服从红色的正态分布

1

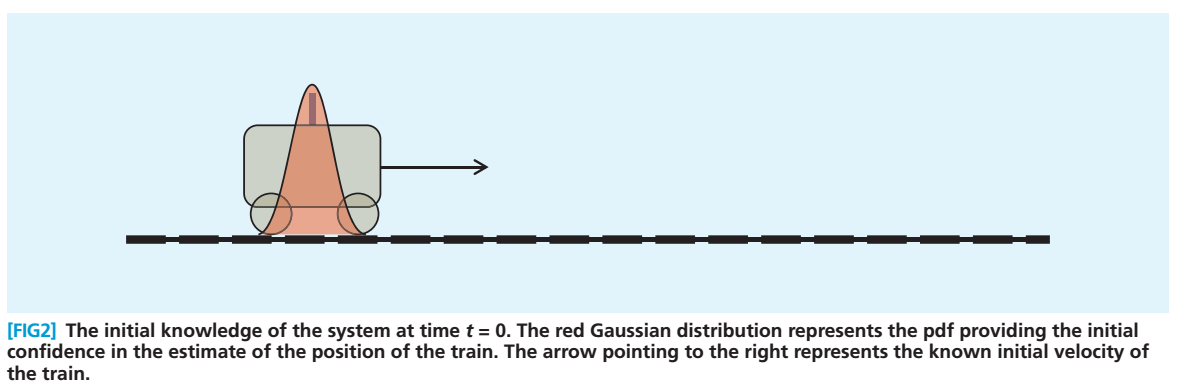
根据小车的位置、运动方向等，我们可以估计出 t=1 时刻它的位置：

2

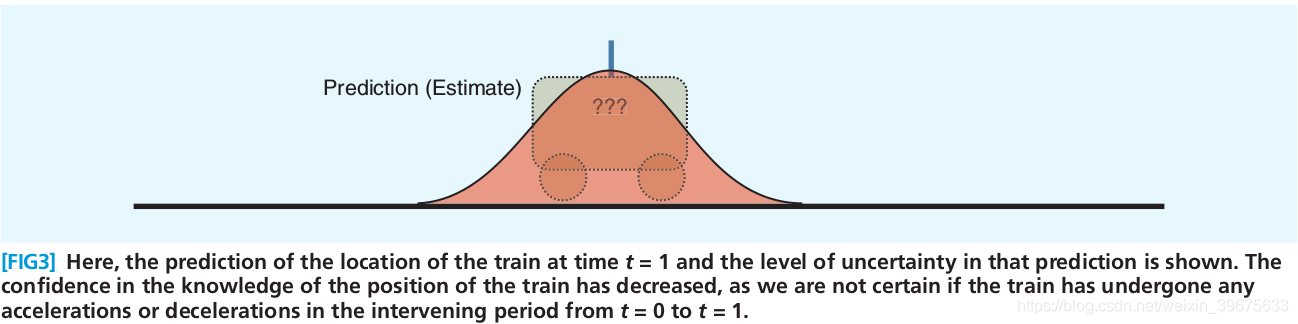
小车位置的分布变宽了，计算的过程中又加了新的噪声，所以不确定性变大了

估计中加入测量（measurement）

3

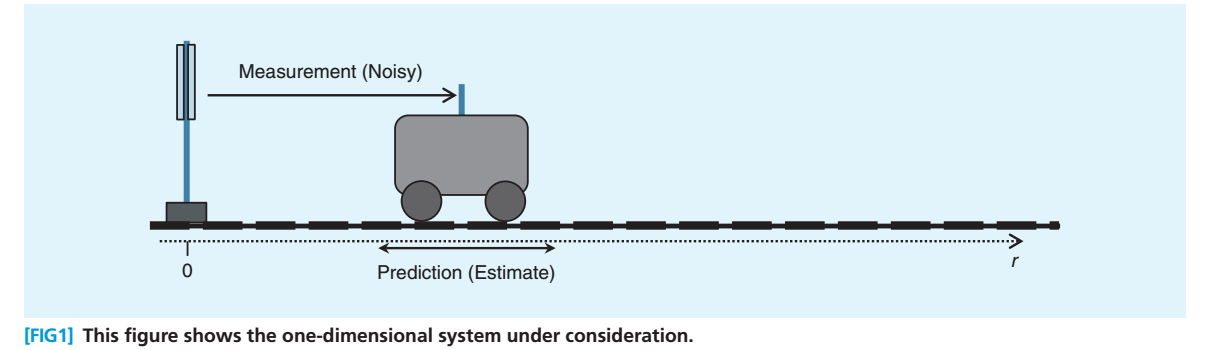
为了避免纯估计带来的偏差，我们在 t=1 时刻对小车的位置坐标进行一次雷达测量，当然雷达对小车距离的测量也会受到种种因素的影响，小车 t=1 时的测量位置服从蓝色的正态分布：

4

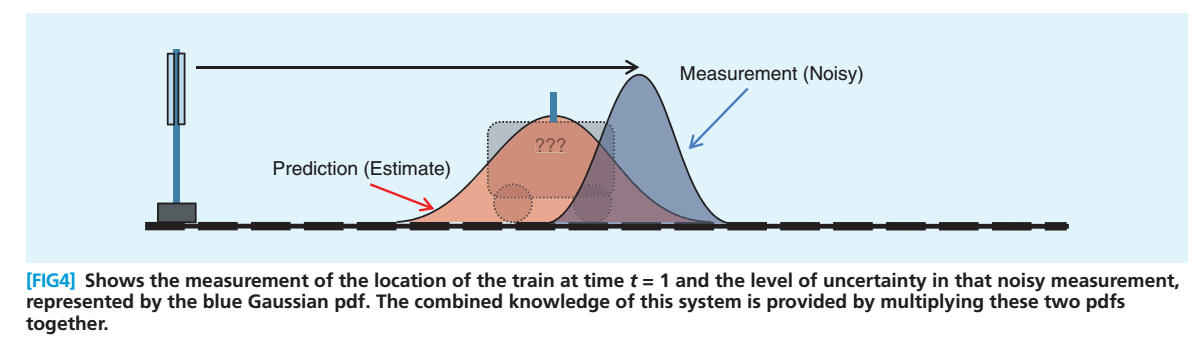
好了，现在我们得到两个不同的结果，估计的结果与测量的结果。Kalman先生，找到了相应权值，加权平均使红蓝分布合并为下图这个绿色的正态分布

5

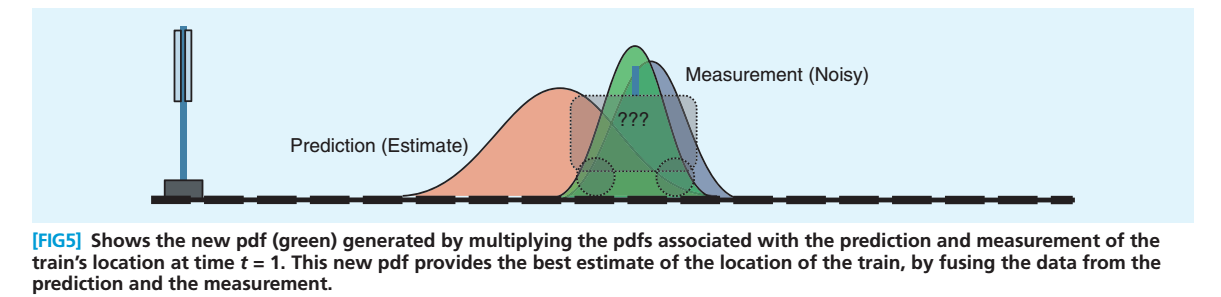
绿色分布不仅保证了在红蓝给定的条件下，小车位于该点的概率最大，而且它还是一个正态分布！

正态分布就意味着，可以把它当做初值继续往下算！这就是 Kalman Filter 迭代的关键，即两个正态分布的融合仍是正态分布！

离散卡尔曼滤波器

1960年，Kalman 发表了他著名的用递归方法解决离散数据线性滤波问题的文章。这部分内容主要来自[2]。

被估计的过程状态

卡尔曼滤波器用于估计离散时间过程的状态变量 x∈Rn 。这个离散时间过程由以下离散随机差分方程描述：

xk=Fk⋅xk−1+Bk⋅uk−1+wk−1

定义观测变量 z∈Rm ，得到测量方程：

zk=Hk⋅xk+vk

随机信号 wk 和 vk 分别表示过程噪声和测量噪声。假设它们相互独立，且服从正态分布：

{p(w)∼N(0,Q)p(v)∼N(0,R)

实际系统中，Q 和 R 可能会随每次迭代计算而变化，为了简单起见，这里的 Q，R 视为常数

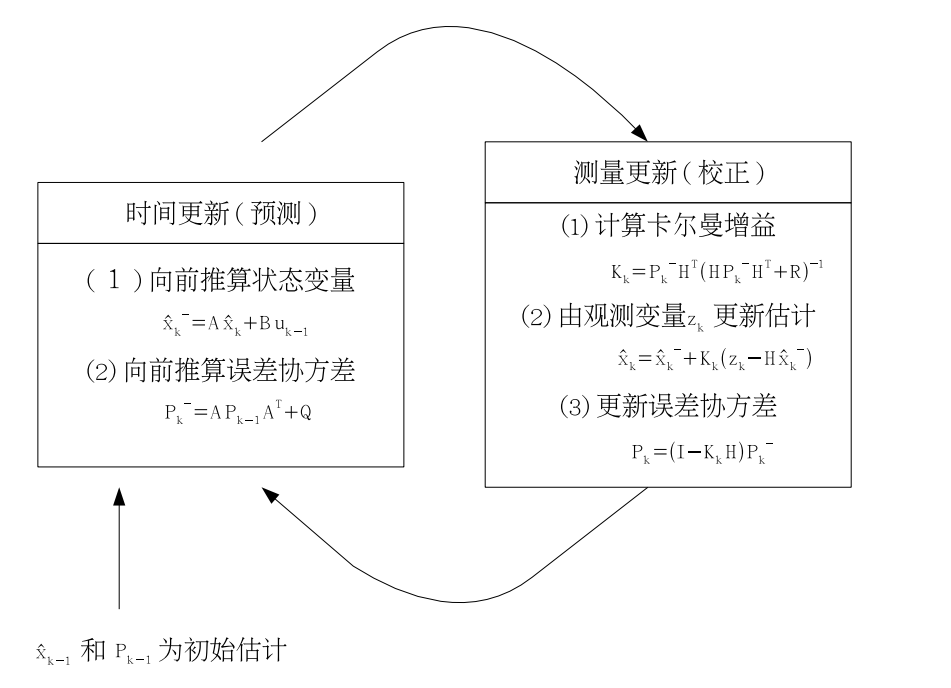
离散卡尔曼滤波器算法

Kalman Filter 用反馈控制的方法估计过程状态：

滤波器估计过程某一时刻的状态，然后以（含噪声的）测量变量的方式获得反馈

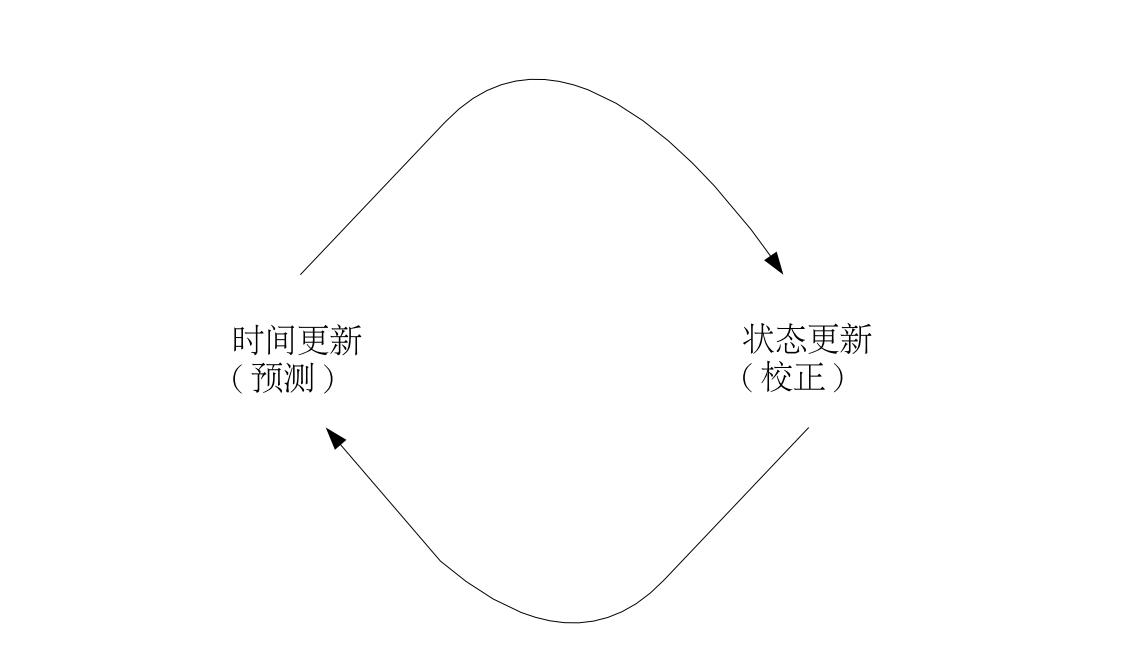
因此 Kalman Filter 可分为两个部分： 时间更新方程和测量（状态）更新方程。

时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计。测量更新方程负责反馈——也就是说，它将先验估计和新的测量变量结合以构造改进的后验估计。

时间更新方程也可视为预估方程，测量更新方程可视为校正方程。最后的估计算法成为一种预估－校正算法 ，如下图所示：

6

时间更新方程

离散卡尔曼滤波器 时间更新方程：

^xk−=F⋅^xk−1+B⋅uk−1
P−k=F⋅Pk−1⋅FT+Q

时间更新方程给出 k 时刻状态的先验估计 ˆx−k 和 先验协方差估计 P−k。

  • ^xk−∈Rn （ − 代表先验，^ 代表估计），为在已知第 k 步以前状态情况下，第 k 步的先验状态估计。
  • ^xk∈Rn 为已知测量变量 zk 时，第 k 步的后验状态估计。
  • F 为将上一时刻 k−1 的状态线性映射到当前时刻 k 的状态转换矩阵，实际中 F 应随时间变化，这里假设为常数。
  • B 为应用于控制向量 uk 的控制输入矩阵，假设为常数。

这里我们提一下先验估计误差和后验估计误差：

{e−k≡xk−^xk−ek≡xk−^xk

这样，先验估计误差和后验估计误差的协方差 P_k^-​ 和 P_k​ 分别为：

{P−k=E[e−ke−kT]Pk=E[ekeTk]

我们简单推导一下 P−k，

P−k=E[(xk−x−k)(xk−x−k)T]

其中 xk−x−k=F⋅xk−1+B⋅uk−1+w−F⋅ˆxk−1−B⋅uk−1=F⋅(xk−1−ˆxk−1)+w，所以：

P−k=E[(F⋅(xk−1−ˆxk−1)+w)(F⋅(xk−1−ˆxk−1)+w)T]

P−k=E[(F⋅ek−1+w)(F⋅ek−1+w)T]

P−k=E[F⋅ek−1⋅wT+F⋅ek−1⋅eTk−1⋅FT+w⋅eTk−1⋅FT+w⋅wT]

因为 ek−1 与 w 不相关，所以 E[F⋅ek−1⋅wT]=E[w⋅eTk−1⋅FT]=0，且 E[w⋅wT]=Q，P−k=E[F⋅ek−1⋅eTk−1⋅FT]+Q，可得：

P−k=F⋅Pk−1⋅FT+Q

测量（状态）更新方程

离散卡尔曼滤波器 测量更新方程：

ˆxk=ˆx−k+Kk(zk−H⋅ˆx−k)
Pk=P−k−Kk⋅H⋅P−k
Kk=P−k⋅HT(H⋅P−k⋅HT+R)−1

测量更新方程首先做的是计算卡尔曼增益 Kk ，然后测量输出以获得 zk ，产生 k 时刻状态的后验估计 ˆxk，最后估计状态的后验协方差 Pk。

后验估计 ˆxk

先验估计 ˆx−k 和 加权的测量变量 zk 及其预测 H⋅ˆx−k 之差的线性组合构成了后验状态估计 ˆxk=ˆx−k+Kk(zk−H⋅ˆx−k) 。

因此 ˆxk 的概率分布取决于在已知先前的测量变量 zk 的情况下， xk 的先验估计 ˆx−k 的概率分布。我们可以看到卡尔曼滤波器表达式中包含了状态变量分布的前二阶矩。

E[xk]=ˆxk

E[(xk−ˆxk)(xk−ˆx)T]=Pk

因为之前假设了过程噪声和测量噪声，相互独立，且服从正态分布，因此状态分布的均值（一阶矩）的估计是正态分布的，后验估计误差协方差则反映了状态分布的方差（二阶非中心矩），这样在已知 zk的情况下， xk 的分布为：

p(xk∣zk)∼N(E[xk],E[(xk−ˆxk)(xk−ˆxk)T])

p(xk∣zk)∼N(ˆxk,Pk)

测量变量及其预测之差 zk−H⋅ˆx−k 反映了测量过程的预测值和实际值之间的不一致程度,为零表明二者完全相同。

卡尔曼增益 Kk

作用是使后验估计误差协方差 Pk 最小，

Kk=P−k⋅HT(H⋅P−k⋅HT+R)−1

Kk=P−k⋅HTH⋅P−k⋅HT+R

可以看到观测噪声协方差 R 越小，zk−H⋅ˆx−k 的增益越大 Kk 越大。当 R 趋向于零时，有：

R→0limKk=H−1

另一方面，先验估计误差协方差 P−k 越小，zk−H⋅ˆx−k 的增益 Kk 越小。当 P−k 趋向于零时，有：

P−k→0limKk=0

这样，增益 Kk 的另一种解释是，随着测量噪声协方差 R 趋于零，测量变量 zk 的权重越来越大，而 zk 的预测 H⋅ˆx−k 的权重越来越小。另一方面，随着先验估计误差协方差 P−k 趋于零，测量变量 zk 的权重越来越小，而 zk 的预测 H⋅ˆx−k 的权重越来越大。

卡尔曼增益 Kk 的推导

最大似然法、Ricatti方程法，以及文章[1]提及的直接对高斯密度函数变形的方法，都可以得到 Kk 。

迭代

计算完时间更新方程和测量更新方程，整个过程再次重复。

上一次计算得到的后验估计被作为下一次计算的先验估计。这种递归推算是卡尔曼滤波器最吸引人的特性之一——它比其它滤波器更容易实现：例如维纳滤波器 [Brown92] ，每次估计必须直接计算全部数据，而卡尔曼滤波器每次只根据以前的测量变量递归计算当前的状态估计。

整个卡尔曼滤波器的过程如下图所示：

7

另一种来自 Wiki 的表示方式如下：

8

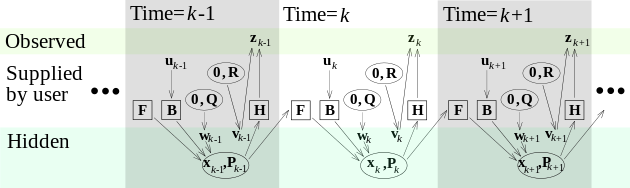
卡尔曼滤波器可以认为是一个时域中离散线性动态系统，可以看做含高斯噪声的误差的线性算子的马尔可夫链（Markov chain）

实践：估计随机常数

这个例子来自文章[2]，Python代码见此。

状态模型

在这个简单的例子里我们估计一个常数随机变量，比如电压。假设我们可以测量这个常数的幅值，但观测幅值中掺

入了幅值均方根（Root-Mean-Square， RMS）为 0.1 伏的白噪声。

过程的状态不随时间变化，所以 F=1；没有控制输入，所以 uk=0； 包含噪声的观测值是状态变量的直接体现，所以 H=1 。

描述状态的线性差分方程变为：

xk=xk−1+w

观测变量为：

zk=xk+v

滤波器方程和参数

时间更新方程为：

ˆx−k=ˆxk−1+w

P−k=Pk−1+Q

测量更新方程为：

Kk=P−k(P−k+R)−1=P−kP−k+R

ˆxk=ˆx−k+Kk(zk−ˆx−k)

Pk=P−k−Kk⋅P−k

假设过程噪声方差 Q 非常小， Q = 10^{−5}（也可以令 Q=0 ，但是一个小的非零常数可以方便地调整滤波器参数，下面将会证明）。再假设由经验我们知道随机常数的真值具有标准正态分布，因此我们令滤波器的初始条件为零，即 \hat{x}_{k−1} = 0 。

类似地，我们要选择 P_{k−1} 的初值 P0 。如果确定初始状态估计 ˆx0=0，可以令 P0=0 。但因为初始状态估计 ˆx0 并不确定，令 P0=0 可能会使滤波器一直产生 ˆxk=0 的结果。就像实验验证的那样， P0 的选择并不关键，
几乎任何 P0≠0 都会使滤波器最终收敛。在这里我们令 P0=1 。

模拟实验

此处请参见文章[2]

Reference

[1] R. Faragher, “Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation [Lecture Notes]”, IEEE Signal Processing Magazine, vol. 29, no. 5, pp. 128–132, Sep. 2012.

[2] G. Welch and G. Bishop, “An Introduction to the Kalman Filter”, p. 16, 2006.

[3] Fitzgerald, Robert J. “Divergence of the Kalman filter”, Automatic Control IEEE Transactions on 16.6(1971):736-747.

[4] 如何通俗并尽可能详细解释卡尔曼滤波？ - 肖畅的回答 - 知乎 https://www.zhihu.com/question/23971601/answer/46480923